• 写在前面
• 问题描述
• 最优性分析
• 稳定性分析
  • LaSalle函数
  • 不变性原理
  • 严格极小值的渐进稳定性

写在前面

原论文标题：Timescale Separation in Autonomous Optimization.

本文为近期阅读的论文(Hauswirth 2020)^[1]和其前作(Menta 2018)^[2]的笔记。该论文研究如图1所示互连反馈系统的稳定性，实际上通过timescale separation假设，直接将物理系统的稳态代入了优化部分，优化部分相当于并未用到状态$x$的反馈。

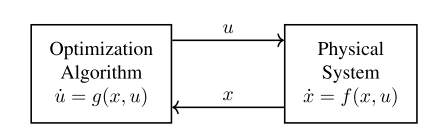
图1. 互连反馈系统

问题描述

这里以线性系统为例。考虑线性时不变(LTI)系统

$\begin{aligned} \dot x&=Ax+Bu+Qw \end{aligned}\qquad (1)$

其中，$x\in\mathbb R^n$，$u\in\mathbb R^p$，$w\in\mathbb R^q$。

假设1： 存在正定矩阵$P\in\mathbb R^{n\times n}$，使得$A^TP+PA\leq-I_n$。

在假设1下，系统(1)指数稳定，$A$可逆，则对固定的$u$和$w$，其稳态为$x=Ku+Rw$，其中$K:=-A^{-1}B\in\mathbb R^{n\times p}$，$R:=-A^{-1}Q\in\mathbb R^{n\times q}$。

考虑稳态输出和控制量的优化问题

$\begin{aligned} \min_{x,u}\quad&\Phi(x,u)\\ \operatorname{s.t.}\quad&x=Ku+Rw, \end{aligned}\qquad (2)$

消除约束，转化为无约束优化问题$\min_u\,\tilde\Phi(u)$，其中$\tilde \Phi(u):=\Phi(Ku+Rw,u)$。根据链式法则(chain rule)，有

$\nabla \tilde \Phi(u):= H^T\nabla\Phi(Ku+Rw,u),$

其中，$H^T:=[K^T,I_n]$。

综上所述，给出如下互连系统

$\begin{aligned} \dot x&=Ax+Bu+Qw，\\ \dot u&=-\alpha H^T\nabla\Phi(x,u)。 \end{aligned}\qquad (3)$

对优化问题$\min\{\Phi(x)|x\in\Omega \}$，其中$\Phi:\mathbb R^n\to \mathbb R$连续可微，点$x^*$称为critial，如果它满足一阶最优条件(KKT条件)，即$x^*\in\Omega$且$-\nabla\Phi(x^*)\in N_\Omega(x^*)$，其中$N_\Omega(x):=\{v\in\mathbb R^n|v^T(y-x)\leq 0,\,\forall y\in\Omega\}$。

若$\Omega=\{x\in\mathbb R^n|h(x)=0,g(x)\leq 0\}$，其中$h:\mathbb R^n\to \mathbb R^s$，$g:\mathbb R^n\to \mathbb R^r$，后一个条件等价于存在$\lambda\in\mathbb R^s$，$\mu\in\mathbb R_+^r$使得

$\nabla \Phi(x^*)+\nabla h(x^*)^T\lambda+\nabla g(x^*)^T\mu=0$

以及$\mu_i g_i(x^*)=0$对所有$i=1,\cdots,r$成立。

试问，互连系统(3)能否将系统(1)控制到优化问题(2)的critical point？

最优性分析

这里首先分析一下互连系统(3)的平衡点是否为优化问题(2)的critical point。

命题1： 优化问题(2)每一个极小值(minimizer)都是互连系统(3)的一个平衡点。反之，互连系统(3)的每一个平衡点都是优化问题(2)的一个critical point。

原论文假设线性无关规范满足，因此KKT条件是局部极小值(local minimizer)的必要条件，可以直接给定local minimizer推导到平衡点。但是无法通过平衡点推导到local minimizer，只能推导到critical point。

给定critical point$(x^*,u^*)$，满足$x^*=Ku^*+Rw$和$\nabla\Phi(x^*,u^*)+[I_n,-K]^T\lambda=0$。

注意到$[I_n,-K]H=0$，因此$H^T\nabla \Phi(x^*,u^*)=0$，$(x^*,u^*)$是互连系统(3)的一个平衡点。

反之，给定平衡点$(x^*,u^*)$，有$x^*=Ku^*+Rw$，且$\nabla \Phi(x^*,u^*)\in \operatorname{ker}H^T=\operatorname{im} H^\bot$。由于$\operatorname{im} H^\bot$由$[I_n,-K]^T$展开，因此$\nabla\Phi(x^*,u^*)+[I_n,-K]^T\lambda=0$。故$(x^*,u^*)$也是critical point。

稳定性分析

假设2： $\tilde \Phi(u)$有$l-$Lipschitz的梯度(gradient)。即$\|H^T(\nabla \Phi(x,u)-\nabla\Phi(x',u))\|\leq l\|x-x'\|$。此外，$\tilde \Phi(u)$的子水平集(sublevel set)是紧集。

如果只知道$\nabla\Phi(x,u)$的lipschitz常数$L$，则取$l:=L\|K\|$可满足条件。

定理1： 在假设1、2下，每当满足

$\alpha<\alpha^*:=\frac{1}{2l\beta}\qquad (4)$

时，互连系统(3)收敛到优化问题(2)的critical point，其中$\beta:=\|PK\|$。此外，只有优化问题(5)的严格local minimizer才是渐进稳定的。

由定理1可以得到，如果优化问题(2)进一步是凸的，那么互连系统(3)收敛到其全局最优解的集合。

我们将定理1的证明分为三个部分。 首先，我们提出了一个LaSalle函数，只要验证了(4)，该函数沿系统的轨迹就不会增加(non-increasing)。 其次，我们应用LaSalle的不变性原理并得出结论，所有轨迹都收敛到满足(2)的一阶最优性条件的点集。 第三，我们证明只有(3)的极小值可以渐近稳定。

LaSalle函数

由singular perturbation analysis启发^[3]，定义如下函数

$Z_\delta(x,u)=(1-\delta)V(u)+\delta W(x,u)， \qquad (5)$

其中$0<\delta<1$是一个凸组合系数，且

$\begin{aligned} V(u)&:=\Phi(Ku+Rw,u)，\\ W(x,u)&:=(x-Ku-Rw)^TP(x-Ku-Rw)。 \end{aligned}$

引理1： $Z_\delta(x,u)$沿着(3)的李导数满足

$\dot Z_\delta(x,u)\leq \begin{bmatrix}\|\psi\|&\|\phi\|\end{bmatrix}\Lambda\begin{bmatrix}\|\psi\|\\ \|\phi\|\end{bmatrix}，$

其中

$\begin{aligned} \psi(x,u)&:=H^T\nabla \Phi(x,u)，\\ \phi(x,u)&:=x-Hu-Rw， \end{aligned}$

以及

$\Lambda:=\begin{bmatrix} -\alpha(1-\delta)&\frac{\alpha}{2}(l(1-\delta)+\delta\beta)\\ \frac{\alpha}{2}(l(1-\delta)+\delta\beta)&-\frac{\delta}{2} \end{bmatrix}。\qquad (6)$

引理2： 考虑(6)中的$\Lambda$，每当$\alpha$满足(4)，那么对一些$\delta^*\in(0,1)$，$\Lambda\leq 0$。

定理1、2证明了$Z_{\delta^*}(x,u)$在条件(4)下不会增加。下面需要证明$\dot Z_{\delta^*}(x,u)$的zero set中的点是否为平衡点，如果是，进一步证明集合的不变性。

不变性原理

以下引理均在$\alpha$满足(4)，$\delta^*$按定理2中定义的条件下给出。

引理3： $\dot Z_{\delta^*}\leq 0$对所有$(x,u)$成立，$\dot Z_{\delta^*}(x,u)=0$当且仅当$(x,u)\in E$，其中

$E=\{(x,u)|x=Ku+Rw,\nabla\Phi(x,u)\in\operatorname{ker} H^T\}。$

此外，$E$中的每一个点都是一个平衡点。

显然，当$\dot Z_{\delta^*}(x,u)=0$时，$\|\psi\|$和$\|\phi\|$都是0，即$(x,u)\in E$。而$\|\psi\|$和$\|\phi\|$为0定义上就是平衡点，所以$E$本身就是平衡点的集合。

引理4： $Z_{\delta^*}(x,u)$的子水平集(sublevel set)对于互连系统(3)是紧集和正不变集。

注意：如果$V(u)\leq c$的子水平集是紧集，那么存在$U$使得$\|u\|\leq U$。

由于$W(x,u)\geq 0$，故$Z_{\delta^*}(x,u)\leq c$是紧的意味着$V(u)\leq c$是紧的。由假设2知，后者确实是紧的，所以$\|u\|\leq U$满足。又由于$V(u)$有下界$L$，$W(x,u)\leq c-L$。因为$P$正定，所以$x$同样有界。

正不变性由$Z_{\delta^*}(x,u)$的非增性保证。

Theorem (LaSalle’s Invariance Principle). Let $\Omega\subset D\subset \mathbb R^n$ be a compact set that is positively invariant with respect to an autonomous system $\dot \eta=F(\eta)$, where $F$ is locally Lipschitz. Let $Z : D\to R$ be a continuously differentiable function such that $\dot Z(\eta)\leq 0$ in $\Omega$. Let $E$ be the set of all the points in $\Omega$ where $\dot Z(η) = 0$. Let $M$ be the largest invariant set in E. Then every solution starting in $\Omega$ approaches $M$ as $t\to\infty$.

因此，轨迹收敛到critical point的集合$E$。

严格极小值的渐进稳定性

假设$z^*:=(x^*,u^*)$是系统(3)的一个渐进稳定平衡点。则$z^*\in\mathcal Z:=\{(x,u)|x=Ku+Rw\}$。

考虑reduced system

$\dot u=-\alpha H^T\nabla\Phi(Ku+Rw,u)。\qquad (7)$

在$z^*$的一个邻域内，起始于$z_0$，系统(3)和(7)的轨迹均收敛于$z^*$，记为$z(t)$和$z'(t)$。区别在于，$z'(t)$永远在$\mathcal Z$内部，而$z(t)$可能先出去再回来。

同时，对于(7)，$\Phi$在其轨迹$z'(t)$上非增，因此$\Phi(z^*)\leq \Phi(z_0)$。因为是$z_0$任意的，所以$z^*$是局部极小值。

假设存在$\bar z$使得$\Phi(\bar z)\leq \Phi(z^*)$。令$z_0=\bar z$，系统(3)的轨迹$z(t)$收敛于$z^*$，$\nabla \tilde \Phi(u(t))=0$对几乎所有$t\geq 0$恒成立。这与$z^*$渐进稳定矛盾。所以渐近稳定点如果存在，必为严格极小值。

---

1. Hauswirth, A., Bolognani, S., Hug, G., & Dörfler, F. (2019). Timescale Separation in Autonomous Optimization. IEEE Transactions on Automatic Control, 1–1. https://doi.org/10.1109/TAC.2020.2989274 ↩︎

2. Menta, S., Hauswirth, A., Bolognani, S., Hug, G., & Dorfler, F. (2019). Stability of Dynamic Feedback optimization with Applications to Power Systems. In 2018 56th Annual Allerton Conference on Communication, Control, and Computing, Allerton 2018 (pp. 136–143). Institute of Electrical and Electronics Engineers Inc. https://doi.org/10.1109/ALLERTON.2018.8635640 ↩︎

3. Khalil, H. K. (2002). Nonlinear systems (3rd ed.). Prentice Hall, ISBN: 0130673897. ↩︎