不等式约束优化问题

凸优化问题根据难度分为三层，不同难度的求解方法不同。第一层可以直接用KKT条件求解，第二层可以用牛顿法求解，以解决带有线性等式约束的优化问题。

本文要讲的内点法(interior-point method)位于第三层，进一步解决优化问题中的不等式约束，如下所示：

\begin{aligned} \min &\quad f_0(x)\\ \operatorname{s.t.} &\quad f_i(x)\leq 0,\quad i=1,\cdots,m\\ &\quad Ax=b, \end{aligned}\quad (1)

其中 $f_0,f_1,\cdots,f_m:\mathbb R^n\to \mathbb R$ 是凸函数，且连续可微；对于 $A\in\mathbb R^{p\times n}$ ， $\operatorname{rank}A=p<n$ 。假设问题(1)可解，即最优解 $x^*$ 存在。记 $f_0(x^*)$ 为 $f_0^*$ 。

假设：问题(1)严格可行(strictly feasible)，即存在 $x\in\mathcal D$ 使得 $Ax=b$ ，所有 $f_i(x)<0$ 成立。

KKT条件：

\begin{aligned} Ax^*=b,\quad f_i(x^*)&\leq 0,\quad i=1,\cdots,m\\ \lambda^*&\geq 0\\ \nabla f_0(x^*)+\sum_{i=1}^m\lambda_i^*\nabla f_i(x^*)+A^T\nu^*&=0\\ \lambda_i^*f_i(x^*)&=0,\quad i=1,\cdots,m. \end{aligned}\quad (2)

对数屏障

为解决问题(1)，我们用罚函数将问题(1)近似为一个等式约束优化问题

\begin{aligned} \min &\quad f_0(x)+\sum_{i=1}^n \mathbb I_-(f_i(x))\\ \operatorname{s.t.}&\quad Ax=b, \end{aligned}

其中， $\mathbb I_-:\mathbb R\to \mathbb R$ 是非正实数的指标函数(indicator function)，

I_-(u)=\left\{ \begin{aligned} 0\quad &u\leq 0\\ \infty \quad &u>0. \end{aligned} \right.

对数屏障算法

定义对数屏障(logarithmic barrier)

\phi(x)=-\sum_{i=1}^m\log(-f_i(x)),

其中定义域 $\operatorname{dom} \phi=\{x\in\mathbb R^n|f_i(x)<0,i=1,\cdots,m \}$ 要求不等式约束严格可行。

引入一个参数 $t>0$ ，可以看出， $\frac{1}{t}\phi(x)$ 是 $I_-(x)$ 的近似。当 $t$ 越大时， $\frac{1}{t}\phi(x)$ 对 $I_-(x)$ 的近似效果越好，如下图所示。实际求解优化问题过程中，可以通过每一步迭代增加 $t$ 的值来达到更好的逼近效果，如：直接令 $t$ 为迭代步数。

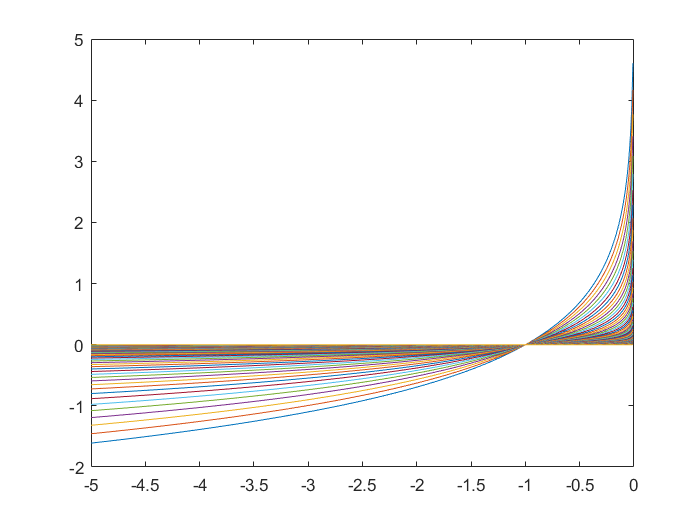
对数屏障函数 $\phi(x)$ 的梯度和Hessian分别为

\begin{aligned} \nabla\phi(x)&=\sum_{i=1}^m\frac{1}{-f_i(x)}\nabla f_i(x),\\ \nabla^2\phi(x)&=\sum_{i=1}^n \frac{1}{f_i^2(x)}\nabla f_i(x)\nabla f_i^T(x)+\sum_{i=1}^m\frac{1}{-f_i(x)}\nabla^2f_i(x). \end{aligned}

令最优解为 $\epsilon$ -optimal，则 $m/t=\epsilon$ 。算法描述如下：

中心路径

考虑优化问题

\begin{aligned} \min &\quad tf_0(x)+\phi(x)\\ \operatorname{s.t.} &\quad Ax=b. \end{aligned}\quad (3)

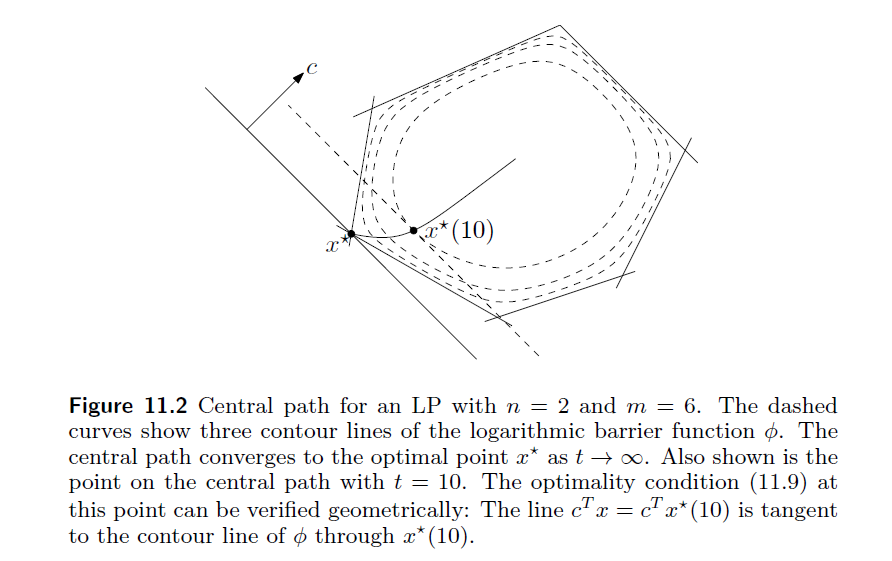
假设问题(3)能用牛顿法解决，且对于每一个 $t>0$ ，问题(3)都有唯一解 $x^*(t)$ 。问题(1)的中心路径(central path)即为中心点 $x^*(t)$ 形成的集合。

点位于中心路径的充分必要条件(centrality condition)为： $x^*(t)$ 严格可行，且存在 $\hat\nu\in \mathbb R^p$ 使得式(4)成立：

\begin{aligned} 0&=t\nabla f_0(x^*(t))+\nabla \phi(x^*(t))+A^T\hat \nu\\ &=t\nabla f_0(x^*(t))+\sum_{i=1}^m\frac{1}{-f_i(x^*(t))}\nabla f_i(x^*(t))+A^T\hat \nu. \end{aligned}\quad (4)

由式(4)可以推出，每一个中心点产生一个对偶可行点。定义

\lambda_i^*(t) = -\frac{1}{tf_i(x^*(t))},\quad i=1,\cdots,m,\quad \nu^*=\frac{\hat \nu}{t}.

则称 $\lambda^*(t)$ 、 $\nu^*(t)$ 对偶可行(dual feasible)。由centrality condition可知， $\lambda^*(t)$ 、 $\nu^*(t)$ 满足前面的KKT条件(2)，故相应的 $x^*(t)$ 也使得拉格朗日函数最小。

对偶函数 $g(\lambda^*(t),\nu^*(t))$ 有界，且

\begin{aligned} g(\lambda^*(t),\nu^*(t))&=f_0(x^*(t))+\sum_{i=1}^m\lambda_i^*(t)f_i(x^*(t))+\nu^*(t)^T(A^Tx^*(t)-b)\\ &=f_0(x^*(t))-m/t\leq f_0^*. \end{aligned}

可知duality gap为 $m/t$ ，且 $f_0(x^*(t))-f_0^*\leq m/t$ ，即 $x^*(t)$ 至少是 $m/t$ -optimal的。

用改进KKT条件解释

改进KKT条件(modified KKT)：对于近似的 $x^*(t)$ ， $x=x^*(t)$ 当且仅当存在 $\lambda,\nu$ 满足

\begin{aligned} Ax^*=b,\quad f_i(x^*)&\leq 0,\quad i=1,\cdots,m\\ \lambda^*&\geq 0\\ \nabla f_0(x^*)+\sum_{i=1}^m\lambda_i^*\nabla f_i(x^*)+A^T\nu^*&=0\\ -\lambda_i^*f_i(x^*)&=1/t,\quad i=1,\cdots,m. \end{aligned}\quad (5)

与式(2)对比，唯一不同的地方是 $\lambda_i^*f_i(x^*)=0$ 换成了 $-\lambda_i^*f_i(x^*)=1/t$ 。

例子：不等式线性规划

考虑LP

\begin{aligned} \min&\quad c^Tx\\ \operatorname{s.t.} &\quad Ax\leq b. \end{aligned}

对数屏障函数

\phi(x)=-\sum_{i=1}^m\log(b_i-a_i^Tx),\quad \operatorname{dom}\phi=\{x|Ax<b\}.

centrality condition

tc+\sum_{i=1}^n\frac{1}{b_i-a_i^Tx}a_i=0.

随着 $t$ 增大，近似最优解逐渐接近真实最优解，形成的轨迹即为中心路径，如下图所示。

改进KKT条件与牛顿法的关系

牛顿法KKT系统

\begin{bmatrix} t\nabla^2 f_0(x)+\nabla^2\phi(x)&A^T\\ A&0 \end{bmatrix}\begin{bmatrix} v_n\\ \nu_n \end{bmatrix}=\begin{bmatrix} -t\nabla f_0(x)-\nabla\phi(x)\\ 0 \end{bmatrix}

将 $\lambda_i = -\frac{1}{tf_i(x)}$ 代入改进KKT条件，解得 $v=v_n$ ， $\nu=\nu_n/t$ 。详见Boyd 2004章节11.3.4^[1]。

对数屏障算法的近似误差

以Mahyar 2018^[2]的时变优化问题为例。只考虑不等式约束

\begin{aligned} \min &\quad f_0(x,t)\\ \operatorname{s.t.} &\quad f_i(x,t)\leq 0,\quad i\in[p]\\ \end{aligned}

其最优解为

x^*(t)=\mathop {\arg \min }\limits_{x \in {R^n}} f_0(x,t)+\sum_{i=1}^p\mathbb I_-(f_i(x,t))\qquad (6)

用对数屏障函数近似的最优解为

\hat x^*(t)=\mathop{\arg\min}\limits_{x\in\hat{\mathcal D}(t)}f_0(x,t)-\frac{1}{c(t)}\sum_{i=1}^p\log(s(t)-f_i(x,t))\qquad (7)

其中 $\hat {\mathcal D}(t):=\{x\in\mathbb R^n|f_i(x,t)<s(t),i\in[p]\}$ 。通过引入松弛变量 $s(t)$ 保证初始时刻 $x(0)\in\hat {\mathcal D}(0)$ 。

假设1 (convexity)：对任意 $t\geq 0$ ， $f_i(x,t),i\in [p]$ 是凸的， $f_0(x,t)$ 是一致强凸的。

假设2 (Slater's Condition)：可行域的内点非空，即存在 $x^\dagger$ 使得 $f_i(x^\dagger,t)<0,i\in[p]$ 成立。

Lemma 1: Let $x^*(t)$ and $\hat x^*(t)$ be defined as in (6) and (7), respectively. Then, under Assumption 1 and 2, and for any $\lambda^*\in \Gamma^*(t)$ and $t\geq 0$ , the following inequality holds:
$|f_0(\hat x^*(t),t)-f_0(x^*(t),t)|\leq \frac{p}{c(t)}+s(t)\left(\inf_{\lambda^*\in\Gamma^*(t)}\|\lambda^*\|_1\right)$

证明：定义

\tilde x^*=\mathop{\arg\min}\limits_{x\in\mathbb R^n}f_0(x,t)+\sum_{i=1}^p\mathbb I_-(f_i(x,t)-s(t))

通过扰动和灵敏度分析(Boyd 2004章节5.6)，当 $s(t)\geq 0$ 时，可建立如下不等式：

0\leq f_0(x^*(t),t)-f_0(\tilde x^*(t),t)\leq \sum_{i=1}^p\lambda_i^* s(t)\qquad(8)

前一个不等式是因为 $s(t)$ 放松了可行域，最优值只会更小不会增加。后一个不等式直接由灵敏度分析得出(Boyd 2004章节5.6)。利用对数屏障函数 $-\frac{1}{c}\log(-u)$ 替代指标函数 $\mathbb I_-(u)$ ，我们可以得到正上界(Boyd 2004章节11)

f_0(\hat x^*(t),t)-f_0(\tilde x^*(t),t)\leq \frac{p}{c(t)}\qquad (9)

由(8)(9)可得，

\begin{aligned} |f_0(\hat x^*(t),t)-f_0(x^*(t),t)|&\leq \frac{p}{c(t)}+\sum_{i=1}^p\lambda_i^* s(t)\\ &\leq \frac{p}{c(t)}+s(t)\left(\inf_{\lambda^*\in\Gamma^*(t)}\|\lambda^*\|_1\right) \end{aligned}

定义

\Phi(x,c,s,t)=f_0(x,t)-\frac{1}{c}\sum_{i=1}^p\log(s-f_i(x,t))

给定prediction-correction算法

\dot x=-\nabla_{xx}^{-1}\Phi(P\nabla_x\Phi+\nabla_{xs}\Phi\dot s+\nabla_{xc}\Phi\dot c+\nabla_{xt}\Phi)\qquad (10)

要使用对数屏障算法，还需要证明 $x(t)\in\hat {\mathcal D}(t)$ 对所有 $t\geq 0$ 成立。

Lemma 2: Let $\hat x^*(t)$ be defined in (7) and $x(t)$ be the solution of (10) for $x(0)\in \hat {\mathcal D}(0)$ , $s(0)>\max_if_i(x(0),0)$ , and $c(0)> 0$ . Then, under Assumptions 1 and 2, $x(t)$ satisfies $x(t)\in \hat {\mathcal D}(t)$ for all $t\geq 0$ . Moreover, the following inequality holds:
$\|x(t)-\hat x^*(t)\|\leq C_3 e^{-\alpha t}$
where $0\leq C_3:=\frac{1}{m_f}\|\nabla _x\Phi(x(0),c(0),s(0),0)\|\leq 0$ 。

证明：因为 $f_0$ 是 $m_f$ -强凸， $c>0$ ， $\Phi$ 在 $\hat {\mathcal D}(t)$ 内也是 $m_f$ -强凸。 $\nabla_{xx}\Phi^{-1}$ 存在且一致有界。将(10)代入闭环动力学，得 $\dot \nabla_x\Phi=-\alpha \nabla_x \Phi$ ，因此 $\|\nabla_x \Phi\|$ 是有界的。注意到

\nabla_x \Phi(x,c,s,t):=\nabla_x f_0(x,t)+\frac{1}{c}\sum_{i=1}^p\frac{\nabla_x f_i(x,t)}{s-f_i(x,t)}，

即在 $\hat {\mathcal D}(t)$ 的边界上 $\|\nabla_x \Phi\|$ 无界。因此由 $\|\nabla_x \Phi\|$ 的有界性可以推出 $x(t)\in \hat {\mathcal D}(t)$ 。再由强凸性得到

\|x(t)-\hat x^*(t)\|\leq \frac{1}{m_f}\|\nabla _x\Phi(x(t),c(t),s(t),t)\|

结合 $\dot \nabla_x\Phi=-\alpha \nabla_x \Phi$ 得证。

Boyd, S., Boyd, S. P., & Vandenberghe, L. (2004). Convex optimization. Cambridge university press. ↩︎
M. Fazlyab, S. Paternain, V. M. Preciado, and A. Ribeiro, “Prediction-correction interior-point method for time-varying convex optimization,” IEEE Trans. Automat. Contr., vol. 63, no. 7, pp. 1973–1986, Jul. 2018. ↩︎

star2dust

凸优化（三）：不等式约束优化算法（内点法）