连续可微和强凸条件
考虑满足如下条件的函数f:
-
梯度单调性(一阶性质):(∇f(x)−∇f(y))T(x−y)≥0,∀x,y∈domf;
-
梯度Lipschitz连续:∥∇f(x)−∇f(y)∥≤L∥x−y∥,∀x,y∈domf。
由第二条知,如下式子等价:
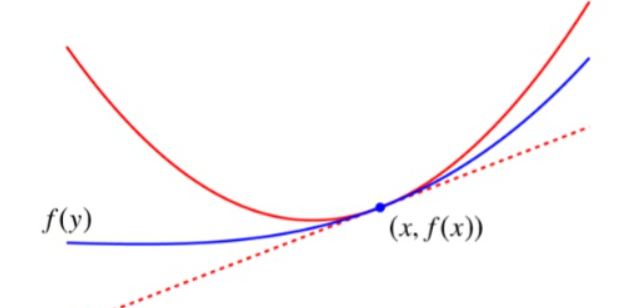
L1∥∇f(x)−∇f(y)∥2f(y)≤(∇f(x)−∇f(y))T(x−y)≤L∥x−y∥2≤f(x)+∇f(x)T(y−x)+2L∥x−y∥2
函数f(y)的上界由二次曲线f(x)+∇fT(x)(y−x)+2L∥x−y∥2确定,称为quadratic upper bound。
满足如下性质的函数称为m-强凸(m-strongly convex)
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)−2mθ(1−θ)∥x−y∥2,
即存在一个m>0使得∇2f(x)≥mI。有如下式子等价:
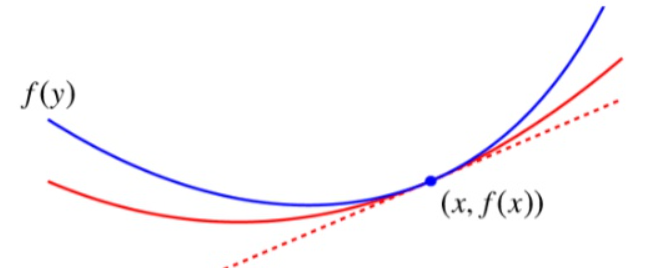
(∇f(x)−∇f(y))T(x−y)≥m∥x−y∥2f(y)≥f(x)+∇f(x)T(y−x)+2m∥x−y∥2
函数f(y)的下界由二次曲线f(x)+∇fT(x)(y−x)+2m∥x−y∥2确定,称为quadratic lower bound。
如果将前面定义中的2m∥x−y∥2换成ϕ(x−y),满足ϕ非负且仅在原点取值为0,则对应的函数f为一致凸(uniformly convex)函数。
无约束优化问题
考虑无约束优化问题minf(x)。常用的方法是梯度下降法:
x˙=−∇f(x).
令Lyapunov函数为V=21∥f(x)−f(x∗)∥2。易证
V˙=−(f(x)−f(x∗))T∇f(x)≤0.
该算法对于次梯度也成立,因为次梯度同样满足凸函数的一阶性质。
如果函数f连续可微和强凸,那么可用牛顿法:
x˙=−∇2f(x)−1∇f(x).
令Lyapunov函数为V=21∥∇f(x)∥2。易证
V˙=−∇f(x)T∇2f(x)∇2f(x)−1∇f(x)≤−2V.
可见牛顿法相对于梯度下降法,有着更快的收敛速度(指数>渐进)。
牛顿法算法
令最优解为ϵ-optimal,算法描述如下:

其中,λ称为牛顿衰减率(Newton decrement),λ(x)=(∇xntT∇2f(x)∇xnt)1/2。
等式约束优化问题
考虑等式优化问题
mins.t.f(x)Ax=b.
将代价函数近似为在x处的二阶泰勒展开
mins.t.f^(x,v)=f(x)+∇f(x)Tv+21vT∇2f(x)vA(x+v)=b.
由KKT条件可得
[∇2f(x)AAT0][vxwx]=[−∇f(x)0],(1)
称为KKT系统,左边的矩阵称为KKT矩阵。
同样,也可以先写出KKT条件,再一阶泰勒展开得到式(1):
∇f(x+vx)+ATwx=∇f(x)+∇2f(x)vx+ATwx=0A(x+vx)=b⟺Avx=0
KKT矩阵非奇异的条件有:
- N(∇2f(x))∩N(A)={0};
- Ax=0,x=0⟹xT∇2f(x)x>0;
- FT∇2f(x)F>0,其中F∈Rn×(n−p)满足R(F)=N(A);
- ∇2f(x)+ATQA>0对有些Q≥0成立。
如果∇2f(x)>0,则KKT矩阵一定非奇异。
令F满足R(F)=N(A)且rankF=n−p,令x^满足Ax^=b。定义
x=Fz+x^,
则可以消去等式约束,得到无约束优化问题和新的代价函数f~(z)=f(Fz+x^),其梯度和Hessian为
∇f~(z)=FT∇f(Fz+x^),∇2f~(z)=FT∇2f(Fz+x^)F.
由牛顿法得到,无约束优化问题的vz=−∇2f~(z)−1∇f~(z)=−(FT∇2f(x)F)−1FT∇f(x).
令vx=Fvz,即vx=−F(FT∇2f(x)F)−1FT∇f(x)。则有
wx=−(AAT)−1A(∇f(x)+∇2f(x)vx).
代入式(1),由于AF=0,故第二行满足。为了证明第一行,我们观察到
[FTA](∇2f(x)vx+ATwx+∇f(x))=0.
因为左边第一个矩阵非奇异,故∇2f(x)vx+ATwx+∇f(x)=0,第一行满足。
综上所述,可以令x˙=vx=−F(FT∇2f(x)F)−1FT∇f(x),就能够保证x收敛到最优解。