• 写在前面
• 问题描述
• 控制器设计
• 时变速度的情况
• 有摩擦力的情况

写在前面

原论文：Cooperative load transport: A formation-control perspective.

本文是Bai 2010^[1]的笔记，主要关注对可变形物体的建模和编队控制思路下的搬运。前两部分是原论文内容，后两部分是我自己的一些想法。

问题描述

假设物体一开始未变形，变形后有如下图近似关系。

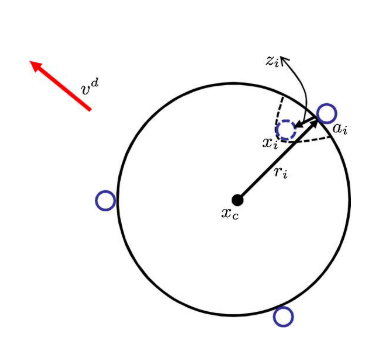
定义变形量

$z_i=x_i-a_i\qquad (1)$

变形产生的应力$f_i$施加到物体上，驱动物体运动。

假设1：$f_i$为一个关于$z_i$强凸正定势函数$P(z_i)$的梯度，即

$f_i=\nabla P_i(z_i)\qquad (2)$

这样定义的应力满足弹簧模型$f_i=k_iz_i$，也满足一些非线性模型，如$f_i=b_i |z_i|^2z_i$，$b_i>0$。

注意，强凸正定条件保证了：

• $P_i(z_i)=\nabla P_i(z_i)=0$当且仅当$z_i=0$。
• 给定$f_i^d$，可以唯一确定$z_i^d$，使得$f_i^d=\nabla P_i(z_i^d)$和$\nabla^2P_i(z_i^d)\geq 0$。

系统模型

$\begin{aligned} m_i\ddot x_i&=F_i-f_i\\ m_o\ddot x_o&=\sum_{i=1}^nf_i \end{aligned}\qquad (3)$

假设2：物体不旋转，即机械臂末端能产生力矩抵消应力带来的旋转力矩。

控制器设计

给定期望速度$v^d$，和期望应力$f_i^d$，满足$\sum_{i=1}^nf_i^d=0$。

设计控制器

$F_i=-\Gamma_i(\dot x_i-v^d)+f_i^d \qquad(4)$

其中$\Gamma_i$正定。下面证明$x_i,x_o\to v^d$以及$f_i\to f_i^d$。

定义李亚普诺夫函数

$V=\sum_{i=1}^n(P_i(z_i)-P_i(z_i^d)-(f_i^d)^T(z_i-z_i^d))+\frac{1}{2}\sum_{i=1}^n\xi_i^Tm_i\xi_i+\frac{1}{2}\xi_o^Tm_o\xi_o\qquad (5)$

其中$\xi_i:=\dot x_i-v^d$和$\xi_o:=\dot x_o-v^d$。

由假设1，可知$V$正定。

对时间求导

$\dot V=\sum_{i=1}^{n}(f_i-f_i^d)^T\dot z_i+\sum_{i=1}^n\xi_i^Tm_i\ddot x_i+\xi_o^Tm_o\ddot x_o\qquad (6)$

由(1)和假设2，有

$\dot z_i=\dot x_i-\dot a_i=\dot x_i-\dot x_o\qquad (7)$

将(3)(4)(7)代入(6)，得到

$\begin{aligned} \dot V&=\sum_{i=1}^{n}(f_i-f_i^d)^T(\dot x_i-\dot x_o)+\sum_{i=1}^n\xi_i^T(-\Gamma_i\xi_i+f_i^d-f_i)+\xi_o^T\sum_{i=1}^nf_i\\ &=-\sum_{i=1}^n\xi_i^T\Gamma_i\xi_i+\xi_o^T\sum_{i=1}^nf_i^d\\ &=-\sum_{i=1}^n\xi_i^T\Gamma_i\xi_i\leq 0 \end{aligned}$

由不变性原理，不变集内部$\xi_i=0$，即$\dot x_i=v^d$。代入(3)得到$F_i=f_i$，再代入(4)得到$f_i^d=f_i$。

下一步证明$\dot x_o=v^d$，由$f_i^d=f_i$可得$z_i^d=z_i$，因此$\dot z_i=0$。代入(7)得到$\dot x_o=\dot x_i=v^d$。

时变速度的情况

给定期望速度$v^d$（时变），和期望应力$f_i^d$（时变），满足$\sum_{i=1}^nf_i^d=m_o\dot v^d$。

设计控制器

$F_i=m_i\dot v^d-\Gamma_i(\dot x_i-v^d)+f_i^d \qquad(8)$

其中$\Gamma_i$正定。下面证明$x_i,x_o\to v^d$以及$f_i\to f_i^d$。

定义李亚普诺夫函数

$V=\sum_{i=1}^n(P_i(z_i)-P_i(z_i^d)-(f_i^d)^T(z_i-z_i^d))+\frac{1}{2}\sum_{i=1}^n\xi_i^Tm_i\xi_i+\frac{1}{2}\xi_o^Tm_o\xi_o\qquad (9)$

其中$\xi_i:=\dot x_i-v^d$和$\xi_o:=\dot x_o-v^d$。

由假设1，可知$V$正定。

对时间求导

$\dot V=\sum_{i=1}^{n}(f_i-f_i^d)^T\dot z_i+\sum_{i=1}^n\xi_i^Tm_i(\ddot x_i-\dot v^d)+\xi_o^Tm_o(\ddot x_o-\dot v^d)\qquad (10)$

由(1)和假设2，有

$\dot z_i=\dot x_i-\dot a_i=\dot x_i-\dot x_o\qquad (11)$

将(3)(8)(11)代入(10)，得到

$\begin{aligned} \dot V&=\sum_{i=1}^{n}(f_i-f_i^d)^T(\dot x_i-\dot x_o)+\sum_{i=1}^n\xi_i^T(-\Gamma_i\xi_i+f_i^d-f_i)+\xi_o^T(\sum_{i=1}^nf_i-m_o\dot v^d)\\ &=-\sum_{i=1}^n\xi_i^T\Gamma_i\xi_i+\xi_o^T(\sum_{i=1}^nf_i^d-m_o\dot v^d)\\ &=-\sum_{i=1}^n\xi_i^T\Gamma_i\xi_i\leq 0 \end{aligned}$

由不变性原理，不变集内部$\xi_i=0$，即$\dot x_i=v^d$。代入(3)得到$F_i=f_i+m_i\dot v^d$，再代入(8)得到$f_i^d=f_i$。

下一步证明$\dot x_o=v^d$，由$f_i^d=f_i$可得$z_i^d=z_i$，因此$\dot z_i=0$。代入(11)得到$\dot x_o=\dot x_i=v^d$。

有摩擦力的情况

系统模型

$\begin{aligned} m_i\ddot x_i&=F_i-f_i\\ m_o\ddot x_o&=\sum_{i=1}^nf_i-b_o\dot x_o-c_o\operatorname{sign}(\dot x_o) \end{aligned}\qquad (12)$

其中$b_o\dot x_o$是粘性摩擦(viscous friction)，$c_o\operatorname{sign}(\dot x_o)$是滑动摩擦(kinetic friction)。

（其实这里应该不是符号函数，而是$\frac{\dot x_o}{\|\dot x_o\|}$。）

给定时变期望速度$v^d$，和时变期望应力$f_i^d$，满足$\sum_{i=1}^nf_i^d=m_o\dot v^d+b_ov^d+c_o\operatorname{sign}(v^d)$。

设计控制器

$F_i=m_i\dot v^d-\Gamma_i(\dot x_i-v^d)+f_i^d \qquad(13)$

其中$\Gamma_i$正定。下面证明$x_i,x_o\to v^d$以及$f_i\to f_i^d$。

定义李亚普诺夫函数

$V=\sum_{i=1}^n(P_i(z_i)-P_i(z_i^d)-(f_i^d)^T(z_i-z_i^d))+\frac{1}{2}\sum_{i=1}^n\xi_i^Tm_i\xi_i+\frac{1}{2}\xi_o^Tm_o\xi_o\qquad (14)$

其中$\xi_i:=\dot x_i-v^d$和$\xi_o:=\dot x_o-v^d$。

由假设1，可知$V$正定。

对时间求导

$\dot V=\sum_{i=1}^{n}(f_i-f_i^d)^T\dot z_i+\sum_{i=1}^n\xi_i^Tm_i(\ddot x_i-\dot v^d)+\xi_o^Tm_o(\ddot x_o-\dot v^d)\qquad (15)$

由(1)和假设2，有

$\dot z_i=\dot x_i-\dot a_i=\dot x_i-\dot x_o\qquad (16)$

将(12)(13)(16)代入(15)，得到

$\begin{aligned} \dot V&=\sum_{i=1}^{n}(f_i-f_i^d)^T(\dot x_i-\dot x_o)+\sum_{i=1}^n\xi_i^T(-\Gamma_i\xi_i+f_i^d-f_i)+\xi_o^T(\sum_{i=1}^nf_i-b_o\dot x_o-c_o\operatorname{sign}(\dot x_o)-m_o\dot v^d)\\ &=-\sum_{i=1}^n\xi_i^T\Gamma_i\xi_i+\xi_o^T(\sum_{i=1}^nf_i^d-b_o\dot x_o-c_o\operatorname{sign}(\dot x_o)-m_o\dot v^d)\\ &=-\sum_{i=1}^n\xi_i^T\Gamma_i\xi_i-\xi_o^Tb_o\xi_o-\xi_o^Tc_o(\operatorname{sign}(\dot x_o)-\operatorname{sign}(v^d))+\xi_o^T(\sum_{i=1}^nf_i^d-b_ov^d-m_o\dot v^d-c_o\operatorname{sign}(v^d)) \end{aligned}$

容易发现$\xi_o^Tc_o(\operatorname{sign}(\dot x_o)-\operatorname{sign}(v^d))\geq 0$，则$\dot V\leq 0$。换成$c_o\xi_o^T(\frac{\dot x_o}{\|\dot x_o\|}-\frac{v^d}{\|v^d\|})$也一样，有

$(\dot x_o-v^d)(\frac{\dot x_o}{\|\dot x_o\|}-\frac{v^d}{\|v^d\|})=(1-\frac{\dot x_o^Tv^d}{\|\dot x_o\|\|v^d\|})(\|\dot x_o\|+\|v^d\|)\geq 0$

由三角不等式，$x^Ty\leq \|x\|\|y\|$，故上述不等式成立。

由不变性原理，不变集内部$\xi_i=0$，即$\dot x_i=v^d$。代入(12)得到$F_i=f_i+m_i\dot v^d$，再代入(13)得到$f_i^d=f_i$。

下一步证明$\dot x_o=v^d$，由$f_i^d=f_i$可得$z_i^d=z_i$，因此$\dot z_i=0$。代入(16)得到$\dot x_o=\dot x_i=v^d$。

没有摩擦的情况，可以令$\sum_{i=1}^nf_i^d=m_o\dot v^d-b_o\xi_o$。剩下的就是load distribution问题了。

---

1. H. Bai and J. T. Wen, “Cooperative load transport: A formation-control perspective,” IEEE Trans. Robot., vol. 26, no. 4, pp. 742–750, Aug. 2010. ↩︎