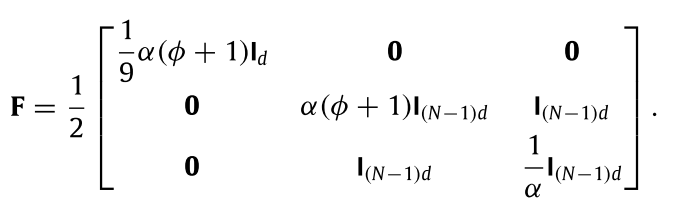• 写在前面
• 分布式算法
• 平衡图收敛性证明

写在前面

原论文：Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication.

上一篇博客：【论文笔记】标准正交基和投影在分布式凸优化中的应用

本文还是Kia 2015^[1]这篇论文的笔记，之前写过一篇关于正交化的笔记，本以为不会再看这篇文章了，没想到有一天会继续填坑。最近在做有向图的分布式优化算法，所以把这篇又捡了起来。

分布式算法

令$\Pi=I_n-\frac{1}{n}1_n 1_n^T$。为了简便表示，可以定义$r\in\mathbb R^n$和$R\in\mathbb R^{n\times (n-1)}$，且满足以下条件：

$r=\frac{1}{\sqrt{n}} 1_n，\,r^TR= 0，\,R^TR=I_{n-1}，\,RR^T=\Pi_n。\qquad (1)$

对每个智能体给定一个代价函数$f_i(x_i)$，满足$\underline m$强凸和$\bar m$光滑，梯度$\nabla f(x)=[\nabla f_1^T(x_1),\cdots,\nabla f_n^T(x_n)]^T$。

定义图$\mathcal G$的拉普拉斯矩阵为$L$。现有动力学如下

$\begin{aligned} \dot v&=\alpha\beta Lx，\\ \dot x&=-\alpha\nabla f(x)-\beta Lx-v， \end{aligned}\qquad (2)$

其中$1_n^Tv(0)=0$。由于$1_n^T\dot v=0$，可以推出$1_n^Tv(t)=1_n^Tv(0)=0$恒成立。由(1)也可知道$r^Tv=0$。

平衡图收敛性证明

定义$P=[r,R]$，其显然是$\mathbb R^n$空间的标准正交基组成的矩阵。由于$P$满秩，所以

$P^TP=PP^T=I_n，\,R^TP=[0_{n-1},I_{n-1}]，\, \Pi P=RR^TP=R[0_{n-1},I_{n-1}]=[0_{n-1},R]。\qquad (3)$

定义$(\bar x,\bar v)$是(2)的平衡点，即

$\begin{aligned} 0&=\alpha\beta L\bar x，\\ 0&=-\alpha\nabla f(\bar x)-\beta L\bar x-\bar v。 \end{aligned}\qquad (4)$

由(4)可知，$\bar x_i=x^*\in\mathbb R^d$，代入第二行，得$\bar v_i=-\alpha\nabla f_i(x^*)=-\alpha\nabla f_i(\bar x_i)$。

为证明平衡点的稳定，定义坐标变换

$\begin{aligned} u&=v-\bar v，\,&y &=x-\bar x，\\ u&=(P\otimes I_d)w，\,&y&=(P\otimes I_d)z。 \end{aligned}\qquad (5)$

由于拉普拉斯矩阵的性质，$P^TLP=\operatorname{diag}( 0,R^TLR)$。简介起见，后面的$R$、$P$和$L$默认做了Kronecker积。

由(1)(5)可知，$w_1=r^TPw=r^Tu=r^T(v-\bar v)=r^T\bar v$，$z_1=r^TPz=r^Ty=r^T(x-\bar x)$。

由(3)可知，$w_{2:n}=R^TPw=R^T(v-\bar v)$，$z_{2:n}=R^TPz=R^T(x-\bar x)$。

定义$h=\nabla f(y+\bar x)-\nabla f(\bar x)$。对(5)左乘$P^T$，得到

$\begin{aligned} \dot w_1&=0，\\ \dot w_{2:n}&=\alpha\beta R^TLRz_{2:n}，\\ \dot z_1&=-\alpha r^T\nabla f(x)=-\alpha r^Th，\\ \dot z_{2:n}&=-\alpha R^T(\nabla f(x)-\nabla f(\bar x))-\beta R^TLRz_{2:n}-R^T(v-\bar v)\\ &=-\alpha R^Th-\beta R^TLRz_{2:n}-w_{2:n}。 \end{aligned}$

考虑李雅普诺夫函数

$V(z,w_{2:n})=\frac{1}{18}\alpha (\phi+1)z_1^Tz_1+\frac{\phi\alpha}{2}z_{2:n}^Tz_{2:n}+\frac{1}{2\alpha}(\alpha z_{2:n}+w_{2:n})^T(\alpha z_{2:n}+w_{2:n})，$

其中$\phi>\max\{4\bar m-1,0\}$。容易看出$V$可以放大成二次型，$V\leq \bar \lambda_F\|p\|^2$，其中$p=[z^T,w_{2:n}^T]^T$，$\bar \lambda_F$是如下矩阵的最大特征值：

对时间求导得

$\begin{aligned} \dot V&=-\frac{1}{9}\alpha^2 (\phi+1)z_1^Tr^Th+\phi\alpha z_{2:n}^T(-\alpha R^Th-\beta R^TLRz_{2:n}-w_{2:n})\\ &\quad+(\alpha z_{2:n}+w_{2:n})^T(-\alpha R^Th-\beta R^TLRz_{2:n}-w_{2:n}+\beta R^TLRz_{2:n})\\ &=-\frac{1}{9}\alpha^2 (\phi+1)z^TP^Th-\frac{7}{16}w_{2:n}^Tw_{2:n}-\phi\alpha \beta z_{2:n}^TR^TLRz_{2:n}\\ &\quad-\frac{8}{9}\alpha^2 (\phi+1)z_{2:n}^TR^Th-\alpha (\phi+1)z_{2:n}^Tw_{2:n}-\alpha w_{2:n}^TR^Th-\frac{9}{16}w_{2:n}^Tw_{2:n}\\ &=-\frac{1}{9}\alpha^2 (\phi+1)y^Th-\frac{7}{16}w_{2:n}^Tw_{2:n}-\phi\alpha \beta z_{2:n}^TR^TL_sRz_{2:n}\\ &\quad+\frac{4}{9}\alpha^2\|R^Th\|^2+\frac{4}{9}\alpha^2(\phi+1)^2z_{2:n}^Tz_{2:n}-\|\frac{3}{4}w_{2:n}+\frac{2}{3}\alpha R^Th+\frac{2}{3}\alpha(\phi+1)z_{2:n}\|^2\\ \end{aligned}$

由于$\|R\|=1$且$\|z\|=\|y\|$，有

$\begin{aligned} &\|R^Th\|^2\leq \|h\|^2\leq \bar my^Th,\\ &y^Th\geq \underline m\|y\|^2=\underline m\|z\|^2. \end{aligned}$

代入$\dot V$得到

$\begin{aligned} \dot V&\leq-\frac{1}{9}\alpha^2 ((\phi+1)-4\bar m)\underline m z^Tz-\frac{7}{16}w_{2:n}^Tw_{2:n}-\phi\alpha \beta \lambda_2 z_{2:n}^Tz_{2:n}\\ &\quad+\frac{4}{9}\alpha^2(\phi+1)^2z_{2:n}^Tz_{2:n}-\|\frac{3}{4}w_{2:n}+\frac{2}{3}\alpha R^Th+\frac{2}{3}\alpha(\phi+1)z_{2:n}\|^2\\ \end{aligned}$

因此$\dot V<-\min\{\frac{7}{16},\frac{1}{9}\gamma \}\|p\|^2<0$，其中$\frac{7}{16}$是$w_{2:n}^Tw_{2:n}$前面的系数，$\frac{1}{9}\gamma$是$z_{2:n}^Tz_{2:n}$前面的系数，$\gamma$具体是多少参看原文。