• 写在前面
• 机械臂模型
• 输入-状态反馈线性化
  • 坐标变换和微分同胚
  • 输入-状态可反馈线性化的条件
  • 机械臂实例1
• 输入-输出反馈线性化
  • 相对阶和李导数
  • 输入-输出可反馈线性化的条件
  • 跟踪控制器设计
  • 机械臂实例2

写在前面

通过反馈和坐标变化来消除系统非线性的控制方法，称为反馈线性化。

反馈线性化(feedback linearization)是用来设计非线性系统(nonlinear systems)控制器的主要方法之一。本文由具有柔性关节的单连杆操纵臂控制实例出发，介绍反馈线性化的基本概念。通过选取不同的系统输出，具有柔性关节的单连杆操纵臂可以是一个相对阶为4没有内部动力学的系统，也可以是相对阶为2的最小相位系统。一个实例足以覆盖本文全部讲解内容，这也是我选择这个实例的原因。一些术语的中文翻译不一定准确，我将必要的英文原文写在后面，实际翻译以专业的参考书为准。

本文并不涉及模型不确定性(model uncertainty)的处理方法，以及不可反馈线性化(not feedback linearizable)的非线性系统控制方法。前者通常以自适应(adaptive)的方法处理，后者可以使用反步法(backstepping)，这两块如果我以后有空会在后续文章里详细讲解。

机械臂模型

考虑竖直平面上的具有柔性关节的单连杆操纵臂(the single-link manipulator with flexible joint)^[1]，其拥有2个自由度，即关节角$\alpha$和电机角$\theta$。假设连杆末端固定有重物，且连杆本身质量相对重物可以忽略不计，重力零点位于连杆最低点。

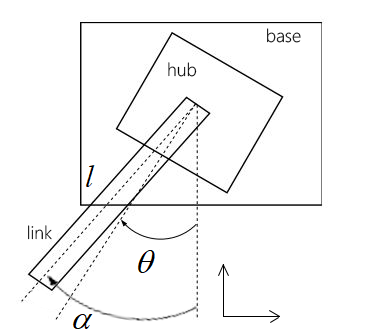
图1. 竖直平面上的具有柔性关节的单连杆操纵臂

用拉格朗日方程求解数学模型，系统的势能(重力$\mathcal V_g$和弹性$\mathcal V_s$)和动能(hub$\mathcal K_h$和link$\mathcal K_l$)为

$\begin{aligned} \mathcal V_g&=mgl(1-\cos \alpha)，\\ \mathcal V_s&=\frac{1}{2}K_s(\alpha-\theta)^2，\\ \mathcal K_h&=\frac{1}{2}J_h\dot \theta^2，\\ \mathcal K_l&=\frac{1}{2}J_o\dot \alpha^2+\frac{1}{2}m(l\dot \alpha)^2， \end{aligned}$

其中$J_h$、$J_o$分别为hub和重物关于各自重心的转动惯量。为了简化变量，定义$J_l=J_o+ml^2$作为link的转动惯量，这也是我们熟悉的平行轴定理。

由$\mathcal L = \mathcal K − \mathcal V$，得到拉格朗日运动方程(Lagrange function of motion)为

$\begin{aligned} \frac{d}{dt}\frac{\partial \mathcal L}{\partial \dot \alpha}-\frac{\partial \mathcal L}{\partial \alpha}&=0，\\ \frac{d}{dt}\frac{\partial \mathcal L}{\partial \dot \theta}-\frac{\partial \mathcal L}{\partial \theta}&=\tau。 \end{aligned}$

经过运算得到数学模型

$\begin{aligned} J_l\ddot \alpha+mgl\sin\alpha+K_s(\alpha-\theta)&=0，\\ J_h\ddot \theta-K_s(\alpha-\theta)&=\tau。 \end{aligned}$

令$x_1=\alpha$,$x_2=\dot \alpha$,$x_3=\theta$,$x_4=\dot \theta$。则有状态空间(state-space)模型

$\begin{bmatrix} \dot x_1\\ \dot x_2\\ \dot x_3\\ \dot x_4 \end{bmatrix}= \begin{bmatrix} x_2\\ -\frac{mgl}{J_l}\sin x_1-\frac{K_s}{J_l}(x_1-x_3)\\ x_4\\ \frac{K_s}{J_h}(x_1-x_3) \end{bmatrix}+ \begin{bmatrix} 0\\ 0\\ 0\\ \frac{1}{J_h} \end{bmatrix}\tau。\qquad(1)$

输入-状态反馈线性化

形如式(1)的非线性系统称为仿射非线性系统(affine nonlinear system)，其一般形式为

$\dot x=f(x)+g(x)u。$

仿射非线性系统最有可能通过状态变换(state transformations)转化为可反馈线性化系统，因为控制量$u$显式出现在动力学中。下面我们针对仿射非线性系统进行分析^[2]。

坐标变换和微分同胚

对于非线性系统，定义坐标变换$z=T(x)$，其中$T:\mathbb R^n\to \mathbb R^n$是微分同胚(diffeomorphism)。也就是说$T$光滑(smooth)，即连续可微，同时$T^{-1}$存在且光滑。

对于线性系统，微分同胚等价于$T$为可逆矩阵，而且该性质是全局(global)的，即在全部$\mathbb R^n$空间成立。而对于非线性系统，全局微分同胚的证明不容易，大多数情况只能证明局部(local)微分同胚，即在一个范围(region)$\Omega\in\mathbb R^n$成立。我们可以通过隐函数定理(implicit function theorem)^[3]证明局部微分同胚的存在性。

引理1：令$T(x)$为范围$\Omega\in\mathbb R^n$上的一个光滑函数。若雅可比矩阵$\nabla T=\frac{\partial T}{\partial x}$在点$x_0\in\Omega$处非奇异(nonsingular)，则$T(x)$在$\Omega$的子范围是一个局部微分同胚。

输入-状态可反馈线性化的条件

非线性系统$\dot x=f(x)+g(x)u$被称为输入-状态可反馈线性化(input-state feedback linearizable)，如果存在一个微分同胚$z=T(x)$，$T(0)=0$，使得

$\dot z=Az+B\beta^{-1}(z)[u-\alpha(z)]，$

其中$(A,B)$可控，且$\beta(z)$是可逆矩阵对所有$z\in \Omega\subset\mathbb R^n$都成立。上式称为$z$-动力学($z$-dynamics)，即非线性系统经过反馈线性化后的正规形式(normal form)。

机械臂实例1

考虑机械臂模型和微分同胚$z=T(x)$

$\begin{aligned} z_1&=x_1，\\ z_2&=x_2，\\ z_3&=-\frac{mgl}{J_l}\sin x_1-\frac{K_s}{J_l}(x_1-x_3)，\\ z_4&=-\frac{mgl}{J_l}x_2\cos x_1-\frac{K_s}{J_l}(x_2-x_4)。 \end{aligned}$

系统在$z$-坐标下的动力学为

$\begin{aligned} \dot z_1&=z_2，\\ \dot z_2&=z_3，\\ \dot z_3&=z_4，\\ \dot z_4&=-z_3\left(\frac{mgl}{J_l}\cos z_1+\frac{K_s}{J_l}+\frac{K_s}{J_h} \right)+\frac{mgl}{J_l}\left(z_2^2-\frac{K_s}{J_h}\right)\sin z_1+\frac{K_s}{J_lJ_h}\tau。 \end{aligned}\qquad (2)$

因此，如果我们选择控制器

$\tau=\frac{J_lJ_h}{K_s}\left[v+z_3\left(\frac{mgl}{J_l}\cos z_1+\frac{K_s}{J_l}+\frac{K_s}{J_h} \right)-\frac{mgl}{J_l}\left(z_2^2-\frac{K_s}{J_h}\right)\sin z_1\right]，$

则可以得到线性系统

$\begin{aligned} \dot z_1&=z_2，\\ \dot z_2&=z_3，\\ \dot z_3&=z_4，\\ \dot z_4&=v。 \end{aligned}$

输入-输出反馈线性化

有时候我们没必要或者无法将非线性系统(1)的全部状态反馈线性化，可以只关心部分状态的组合作为系统的输出，于是有输入-输出反馈线性化(input-output linearization)的概念。

相对阶和李导数

考虑单输入单输出(SISO)非线性系统

$\begin{aligned} \dot x&=f(x)+g(x)u，\\ y&=h(x)， \end{aligned}\qquad (3)$

其中$u\in\mathbb R$，$y\in\mathbb R$，$x\in\mathbb R^n$，且$f,g,h$在域(domain)$D\subset\mathbb R^n$上充分光滑(sufficiently smooth)。

注意：这里之所以说充分光滑，是因为没有必要$C^\infty$。若相对阶为$r$，保证$C^r$即可。

求得$y$关于时间的导数为

$\dot y=\frac{\partial h}{\partial x}(x)f(x)+\frac{\partial h}{\partial x}(x)g(x)u。$

如果$\frac{\partial h}{\partial x}(x)g(x)\neq 0$对任意$x\in D_0$成立，那么该非线性系统被称为在域$D_0$上相对阶(relative degree)为1。也就是说，$u$显式出现(explicitly appear)在$\dot y$中，而当$u$显式出现在$y$中时，我们称该非线性系统相对阶为0。如果$\frac{\partial h}{\partial x}(x)g(x)= 0$，那么我们继续求导，直到$u$第一次显式出现。

为了方便重复求导，我们定义李导数(Lie derivative)。函数$h$关于(with respect to)$f$的李导数记作

$L_fh(x)=\frac{\partial h}{\partial x}(x)f(x)。$

基于李导数，我们有

$\begin{aligned} L_f^k h(x)&=L_fL_f^{k-1}h(x)=\frac{\partial}{\partial x}(L_f^{k-1}h(x))f(x)，\\ L_gL_f^k h(x)&=\frac{\partial}{\partial x}(L_f^kh(x))g(x)。 \end{aligned}$

如果$L_g h(x)=0$，即相对阶大于1，那么继续求导直到$L_gL_f^{r-1}h(x)\neq 0$在$r$时第一次成立，即$u$显式出现在$y$的$r$阶导数$y^{(r)}$中，此时称该非线性系统的相对阶为$r$。

输入-输出可反馈线性化的条件

如果非线性系统相对阶为$r$，那么$L_gL_f^i h(x)=0$，$\forall i = 1,2,\cdots,r-2$，同时$y^{(r)}=L_f^rh(x)+L_gL_f^{r-1}h(x)u$。此时$y$系统输入-输出可反馈线性化(input-output linearizable)，相应的状态反馈控制器为

$u=\frac{1}{L_gL_f^{r-1}h(x)}\left[v-L_f^rh(x)\right]。$

除非$r=n$，该非线性系统仍有部分状态不受$u$控制，剩下的$(n-r)$个状态定义了该非线性系统的零动力学(zero dynamics)。对于一个相对阶为$r$的系统，存在微分同胚$z=T(x)$使得非线性系统(3)转化为输入-输出可反馈线性化标准型(input-output linearizable canonical form)

$\begin{aligned} \dot \eta&=\phi(\eta,\zeta)，\\ \dot \zeta&=A_0\zeta+B_0\beta_0^{-1}(\eta,\zeta)\left[u-\alpha_0(\eta,\zeta)\right]，\\ y&=C_0\zeta， \end{aligned}$

其中$z=[\eta^T,\zeta^T]^T$，$\eta\in\mathbb R^{n-r}$，$\zeta\in\mathbb R^r$，且$(A_0,B_0,C_0)$是标准型

$A_0=\begin{bmatrix} 0&1&0&\cdots&0\\ 0&0&1& &0\\ \vdots& & &\ddots &\vdots\\ 0& & & &1\\ 0&0&&\cdots&0 \end{bmatrix}, B_0=\begin{bmatrix} 0\\ 0\\ \vdots\\ 0\\ 1 \end{bmatrix}, C_0=\begin{bmatrix} 1&0&\cdots&0&0 \end{bmatrix}。$

由此可见非线性系统的正规形式被分解为(decomposed in)两部分，即能够被反馈线性化的$\zeta$-动力学，以及表征(characterize)内部动力学(internal dynamics)的$\eta$变量(variables)。$\zeta$-动力学对应的反馈控制器为

$u=\alpha_0(\eta,\zeta)+\beta_0(\eta,\zeta)v，\qquad (4)$

其中

$\alpha_0(\eta,\zeta)=\left.\frac{L_f^r h(x)}{L_gL_f^{r-1}h(x)}\right|_{x=T^{-1}(\eta,\zeta)}, \beta_0(\eta,\zeta)=\left.\frac{1}{L_gL_f^{r-1}h(x)}\right|_{x=T^{-1}(\eta,\zeta)}$

零动力学通过在$\eta$-动力学中设置$\zeta=0$得到：$\dot \eta=\phi(\eta,0)$，其不可观也无法被$u$控制，需要其自身具有一定的稳定属性（不一定非要渐进稳定）。

非线性系统(3)被称为最小相位(minimum phase)，如果零动力学在域$D$上有一个渐近稳定的平衡点(asymptotically stable equilibrium)。

注意：1. 线性系统也可能有相对阶，即$r\neq n$，但是其零动力学也是线性的；2. 非线性系统的相对阶可能不明确(undefined)，尤其当$L_gL_f^i h(x)=0$对某些$x$取值成立（即奇异点），此时该非线性系统不可转化为输入-输出可反馈线性化标准型。

跟踪控制器设计

假设控制目标(control objective)是让$y(t)$跟踪一个期望信号$y_d(t)$。令$e(t)=y(t)-y_d(t)$是跟踪误差。设计反馈控制器(4)，其中$v$选择如下：

$\begin{aligned} v &= y_d^{(r)}-k_{r-1}e^{(r-1)}-\cdots-k_1\dot e-k_0e\\ &=y_d^{(r)}-\sum_{j=0}^{r-1}k_j\left(L_f^j h(x)-y_d^{(j)} \right)。 \end{aligned}$

注意：为什么没有$L_gL_f^{j-1} h(x)$?因为$L_gL_f^i h(x)=0$，$\forall i = 1,2,\cdots,r-2$。

代入该反馈控制器，得到线性误差动力学

$e^{(r)}+k_{r-1}e^{(r-1)}+\cdots+k_1\dot e+k_0e=0。$

通过合理选择参数(coefficients)$\{k_0,k_1,\cdots,k_{r-1}\}$，特征方程(characteristic equation)

$s^{(r)}+k_{r-1}s^{(r-1)}+\cdots+k_1s+k_0=0$

的根(root)可以任意分配(assign)。这意味着跟踪误差可以以指数速率(expoentially fast)渐进收敛于0。

下面考虑内部动力学$\dot \eta=\phi(\eta,\zeta)$。令

$\bar y_d(t)=\begin{bmatrix} y_d(t)&\dot y_d(t)&\cdots&y_d^{r-1}(t) \end{bmatrix}^T。$

假设$\bar y_d(t)$对所有$t\geq 0$有界(bounded)，且$\dot \eta=\phi(\eta,\bar y_d(t))$的解意义明确(well defined)、有界，且一致(uniformly)渐进稳定，那么该反馈控制器保证全部状态有界，且跟踪误差指数收敛于0。

机械臂实例2

考虑与上节相同的机械臂模型。首先考虑输出$y=x_1$，该情况下相对阶为4，与状态变换后的非线性系统(2)阶数相同，因此没有内部动力学。

下面考虑输出$y=x_3$。对$y$求导数，

$\begin{aligned} \dot y &= x_4，\\ \ddot y &= \frac{K_s}{J_h}(x_1-x_3)+\frac{1}{J_l}\tau。 \end{aligned}$

因此，该情况下相对阶为2。设计反馈控制器为

$u=J_l\left(\ddot y_d-\frac{K_s}{J_h}(x_1-x_3)-\lambda_1(y-y_d)-\lambda_2(\dot y-\dot y_d)\right)，$

其中$\lambda_1,\lambda_2>0$。零动力学为

$\begin{aligned} \dot x_1 &= x_2，\\ \dot x_2 &= \frac{mgl}{J_1}\sin x_1+\frac{K_s}{J_l}x_1， \end{aligned}$

即$J_l\ddot \alpha+mgl\sin\alpha+K_s\alpha=0$，显然渐进稳定于原点。

---

1. Groves, K., & Serrani, A. (2010). Modeling and Nonlinear Control of a Single-link Flexible Joint Manipulator, (3), 13. Retrieved from https://www2.ece.ohio-state.edu/~passino/lab5prelabnlc.pdf ↩︎

2. Khalil, H. K. (2002). Nonlinear systems (3rd ed.). Prentice Hall, ISBN: 0130673897. ↩︎

3. Farrell, J. A., & Polycarpou, M. M. (2006). Adaptive Approximation Based Control. Wiley Press. Hoboken, NJ, USA: John Wiley & Sons, Inc. https://doi.org/10.1002/0471781819 ↩︎