• 阻抗模型
• 物体阻抗
• 分布阻抗
• MATLAB和RTB仿真
  • 物体阻抗
  • 分布阻抗
• 源代码

阻抗模型

阻抗控制的目的是将原有物体动力学修正为我们期望动力学。假设有一个弹簧，通过阻抗控制，可以使得它的刚度降低，实际推它时有可能感觉像一个海绵。

阻抗模型期望动力学一般为线性二阶系统

$M_d(\ddot X_o-\ddot X_o^d)+K_v(\dot X_o-\dot X_o^d)+K_p(X_o-X_o^d)=F_{ext}，$

其中，$F_{ext}$为外力(external force)，系数$M_d$、$K_v$、$K_p$针对每个自由度独立指定（对角阵）。

阻抗模型的一般形式

$M_d\ddot X_o=F_{ext}+F_{imp}，$

其中，$F_{imp}$是虚阻抗力(imaginary impedance force)，既可以模拟动力学，也可以模拟力。仅用于模拟动力学时可以取

$F_{imp}=M_d\ddot X_o^d-K_v(\dot X_o-\dot X_o^d)-K_p(X_o-X_o^d)。$

物体阻抗

由牛顿欧拉公式可得

$\begin{aligned} m_o\ddot x_o&=f_{ext}+\sum f_{cmd}^i+m_og\\ \mathcal I_o\dot \omega_o+\omega_o\times\mathcal I_o\omega_o&=\tau_{ext}+\sum r_i\times f_{cmd}^i+\sum\tau_{cmd}^i \end{aligned}$

假设实际物体动力学

$M_o\ddot X_o+C_o=F_{ext}+G\boldsymbol F_{cmd}，$

其中$M_o=\begin{bmatrix}m_oI_3&0_3\\0_3&\mathcal I_o\end{bmatrix}$，$C_o=\begin{bmatrix}-m_og\\\omega_o\times\mathcal I_o\omega_o\end{bmatrix}$是惯性矩阵和哥氏矩阵，$G$是抓持矩阵(grasp matrix)，通常为

$G=\begin{bmatrix} I_3&0&I_3&0&\cdots&I_3&0\\ S(r_1)&I_3&S(r_2)&I_3&\cdots&S(r_n)&I_3 \end{bmatrix}。$

这里注意三点：

• 上述物体动力学是在基坐标系下定义的，所以牛顿欧拉方程的牛顿部分非常简单
• 由此而产生的不便之处是，$G$是时变的，因为$r$在基坐标系下时变（随物体旋转）
• 可以将上述物体动力学定义在物体坐标系下，这样$G$是常数矩阵^[1]

期望的物体动力学，即物体阻抗^[2](object impedance），具有compliant behavior，

$M_d\ddot X_o=F_{ext}+F_{imp}。$

联立两式

$G\boldsymbol F_{cmd} = C_o-F_{ext}+M_oM_d^{-1}(F_{ext}+F_{imp})。$

控制力(commanded forces)为

$\boldsymbol F_{cmd}=G^\dagger[C_o-F_{ext}+M_oM_d^{-1}(F_{ext}+F_{imp})]+\boldsymbol F_{int}，$

其中$\boldsymbol F_{int}$为内力(internal forces)，在$G$的零空间(null space)中。

分布阻抗

上节的物体阻抗方法将物体和机械臂考虑为一个整体，在物体层面(object level)进行集中式控制，但是集中式控制有如下弊端。

Such a centralized approach implies that specific pieces of hardware share data in real time from each manipulator force and position sensor. Notice that the structure of the controller depends on the system. This almost prohibits the implementation of regrasp- ing procedures or, more generally, any change in the system topology. Furthermore, when the system is built-up by manipulators with heterogeneous performance, the whole system performance reflects that of the worst one, especially for precision and stability^[3].

考虑分布式控制，可以在关节层面(joint level)和末端执行器层面(end-effector level)进行控制。末端执行器层面的控制有很多，如Leader-follower approach和Master-slave approach，前者是纯位置控制，后者master进行位置控制，slave进行力控制。

分布阻抗(distributed impedance)是在末端执行器层面的控制。由于多机械臂的冗余性，末端执行器可以通过点接触只控制力$f$，无需控制力矩$\tau$。

假设实际物体动力学

$M_o\ddot X_o+C_o=F_{ext}+G\boldsymbol f，$

其中，

$G=\begin{bmatrix} I_3&I_3&\cdots&I_3\\ S(r_1)&S(r_2)&\cdots&S(r_n) \end{bmatrix}。$

则实际末端速度为

$\dot {\boldsymbol x}=G^T\dot X_o。$

末端期望的力为

$\boldsymbol f=G^\dagger(M_o\ddot X_o+C_o-F_{ext})+\boldsymbol f_{int}。$

末端期望阻抗模型为

$-f_i=M_d^i\ddot x_i+B_d^i(\dot x_i-\dot x_d^i)+K_d^i(x_i-x_d^i)，$

其中，$f_i$是末端输出的力，因此取负号才是受到的力。

定义$e_i=x_d^i-x_i$，上式的拉普拉斯变换为

$L_f(s)=(B_d^is+K_d^i)L_e(s)。$

当期望力看作常值时，为阶跃响应函数，有

$\lim_{s\to 0}sL_e(s)=\lim_{s\to 0}s(B_d^is+K_d^i)^{-1}(f_i/s)=\lim_{s\to 0}(B_d^is+K_d^i)^{-1}f_i=K_d^{i^{-1}}f_i。$

期望的稳态末端轨迹与实际接触点轨迹之间的关系为

$x_d^i=x_i+K_d^{i^{-1}}f_i。$

机械臂末端速度和加速度有如下关系

$\dot q_i=J_i^{-1}\dot x_i，\quad \ddot q_i=J_i^{-1}\ddot x_i-J_i^{-1}\dot J_i\dot q_i=J_i^{-1}\ddot x_i-J_i^{-1}\dot J_iJ_i^{-1}\dot x_i，$

其中$J_i^{-1}=M_i^{-1}J_i^T(J_iM_i^{-1}J_i^T)^{-1}$。

将阻抗模型代入机械臂末端动力学

$J_i^{-T}\tau_{cmd}^i-f_i=\tilde M_i(q_i)\ddot x_i+\tilde C_i(q_i,\dot q_i)\dot x_i+\tilde N_i(q_i)，$

其中，$\tilde M_i=J_i^{-T}M_iJ_i^{-1}$，$\tilde C_i=J_i^{-T}\left(C_iJ_i^{-1}+M_iJ_i^{-1}\dot J_iJ_i^{-1}\right)$，$\tilde N_i=J^{-T}N_i$。

控制力矩为

$\tau_{cmd}^i=J_i^T\left[-\tilde M_iM_d^{i^{-1}}(B_d^i(\dot x_i-\dot x_d^i)+K_d^i(x_i-x_d^i))+\tilde C_i\dot x_i+\tilde N_i+(I_3-\tilde M_iM_d^{i^{-1}})f_i\right]$

MATLAB和RTB仿真

使用RTB工具箱建模二自由度机械臂，在竖直平面内搬运一个方块。

首先是机械臂建模和方块物体建模，代码示例如下。

%% robot modeling
lx = 1; lr = 0.1; g = [0 -9.81 0]; fvis = 0; fcou = 0; 
rod = Cuboid([lx,lr,lr]);
Irod = rod.inertia;
dpm = {'a', lx, 'm', rod.mass, 'r', [-lx/2,0,0], 'qlim', [-pi/2, pi/2],'I', Irod,...
    'B', fvis, 'Tc', [fcou -fcou]};
rob(1) = SerialLink([Revolute(dpm{:}),Revolute(dpm{:})],'name','r1','gravity',...
    -g,'base',SE3([-1,0,0]/2));
rob(2) = SerialLink([Revolute(dpm{:}),Revolute(dpm{:})],'name','r2','gravity',...
    -g,'base',SE3([1,0,0]/2));
%% object modeling
obj = Cuboid([lx,lx,lr]);

然后定义几何位置关系，代码示例如下。

%% joint positions (x,y)
x0 = [-1,1.5,0;
    0,1.5,0];
for i=1:2
   q(i,:) = rob(i).ikine(SE3(x0(i,:)),'mask',[1,1,0,0,0,0]); 
end
q(1,:) = [sum(q(1,:)),-q(1,2)];
dq = zeros(size(q));
qd = q;

%% object position (x,y,z,r,p,y)
Xo = [sum(x0)/size(x0,1),0,0,0];
dXo = zeros(1,6);
ddXo = dXo;
for i=1:2
   ro(i,:) = x0(i,:)-Xo(1:3);
end

%% object dynamics
Mo = blkdiag(obj.mass*eye(3),obj.inertia);
Co = @(dXo) [-obj.mass*g';skew(dXo(4:6))*obj.inertia*dXo(4:6)'];
r = @(Xo,i) (SO3.rpy(Xo(4:6))*ro(i,:)')';
G = @(Xo) [eye(3),eye(3);
    skew(r(Xo,1)),skew(r(Xo,2))];

物体阻抗

控制力由如下代码给出

%% command force
Fcmd = @(Xo,dXo,Xd) (pinv(G(Xo))*(Co(dXo)+Mo*md^-1*Fimp(Xo,dXo,Xd)')+Fint(Xo)')'; 

仿真结果如下图所示。

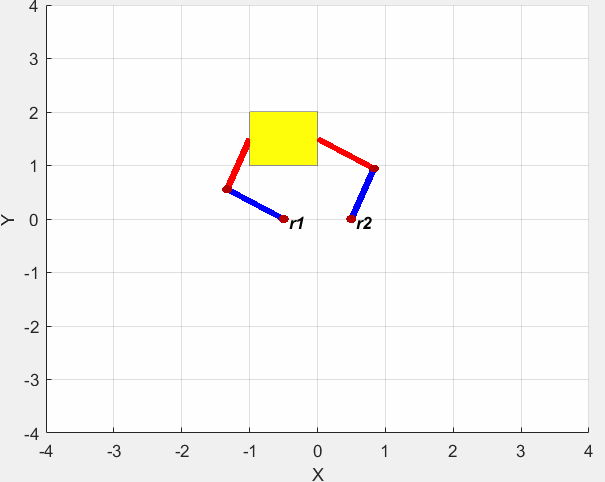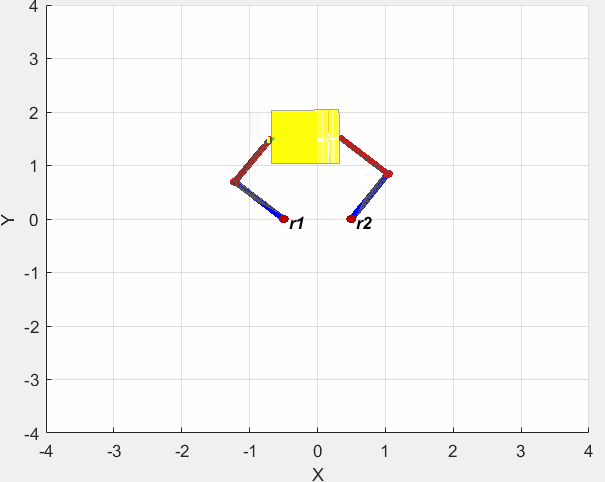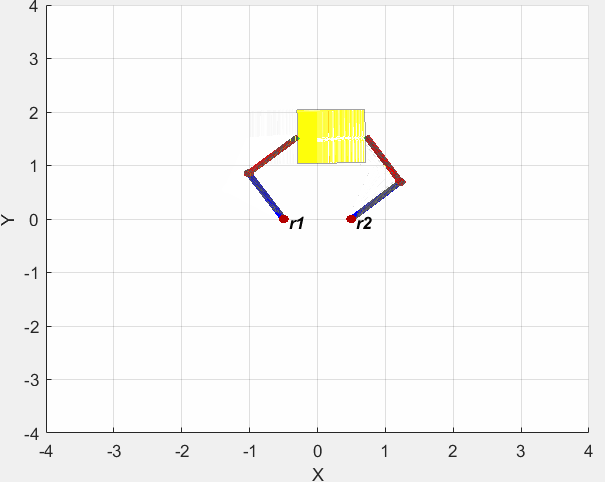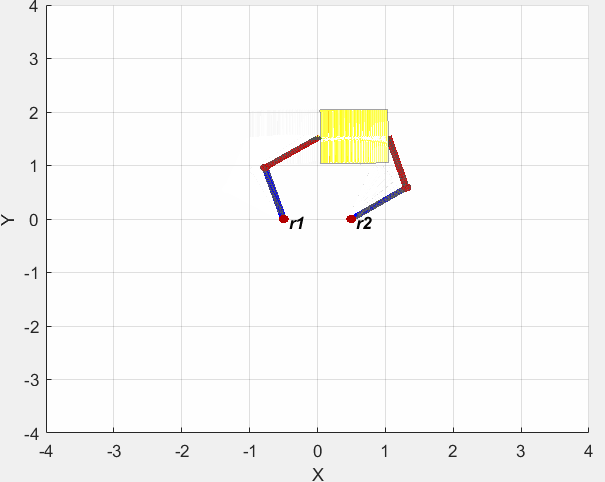
分布阻抗

控制力由如下代码给出

%% command force
Fcmd = @(Xo,dXo,Xd) (pinv(G(Xo))*(Co(dXo)+Mo*ddXo(Xo,dXo,Xd,dXd)')+Fint(Xo)')'; 

控制力矩由如下代码给出

md = 3; kv = 15; kp = 25; F = Fcmd(Xo,dXo,Xd); 

% end-effector trajectory
J = rob(i).jacob0(q(i,:),dq(i,:)); J(3:6,:)=[];
Jdq = rob(i).jacob_dot(q(i,:),dq(i,:)); Jdq(3:6,:)=[];
x(i,:) = rob(i).fkine(q(i,:)).t;
dx(i,:) = J*dq(i,:)';

% desired trajectory
xd(i,:) = Xo(1:3)+(SO3.rpy(Xo(4:6))*ro(i,:)')'+F(3*i-2:3*i)/kp;
dxd = reshape((G(Xo)'*dXo')',[3,2])';

% joint torque
Mq = rob(i).inertia(q(i,:)); 
Cq = rob(i).coriolis(q(i,:),dq(i,:));
Gq = rob(i).gravload(q(i,:))';
Jinv = Mq^-1*J'*(J*Mq^-1*J')^-1;
Mx = Jinv'*Mq*Jinv;
Cx1 = Jinv'*Cq*Jinv;
Cx2 = Jinv'*Mq*Jinv*Jdq;
Gx = Jinv'*Gq;
tau(i,:) = J'*(-Mx*md^-1*(kv*(dx(i,1:2)-dxd(i,1:2))+kp*(x(i,1:2)-xd(i,1:2)))'+...
Cx1*dx(i,1:2)'+Cx2+Gx+(eye(2)-Mx*md^-1)*F(3*i-2:3*i-1)');

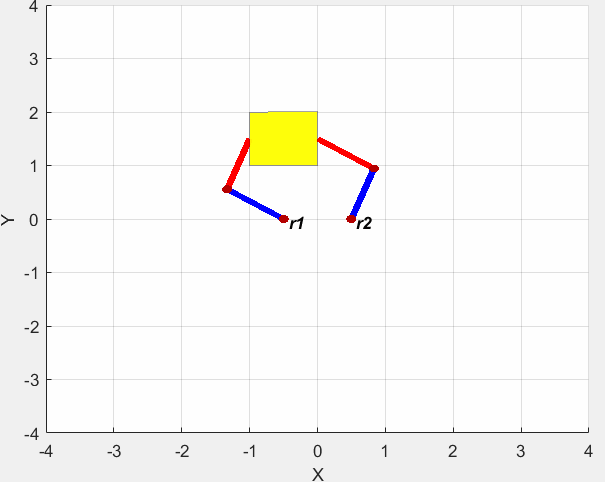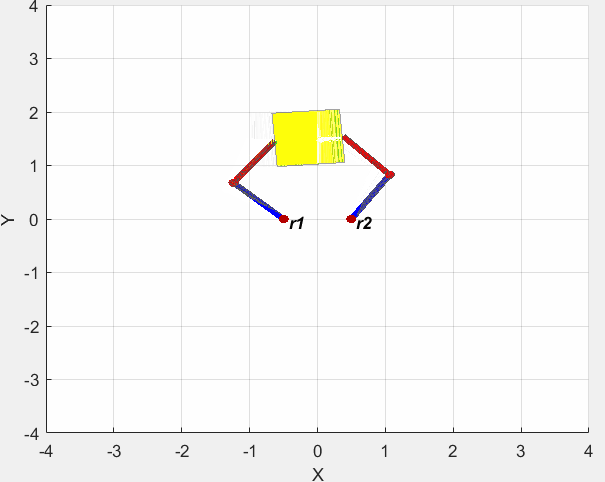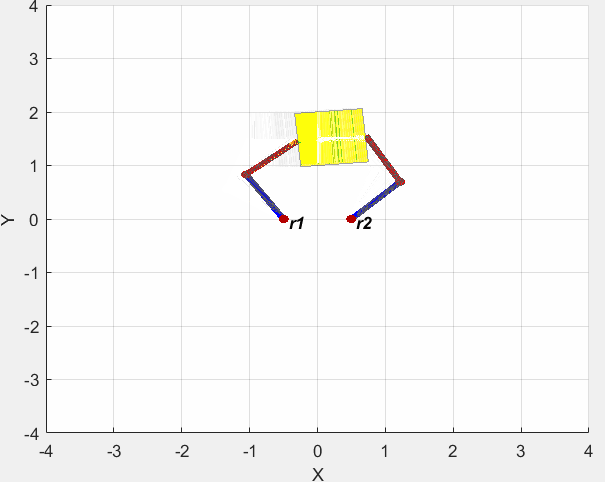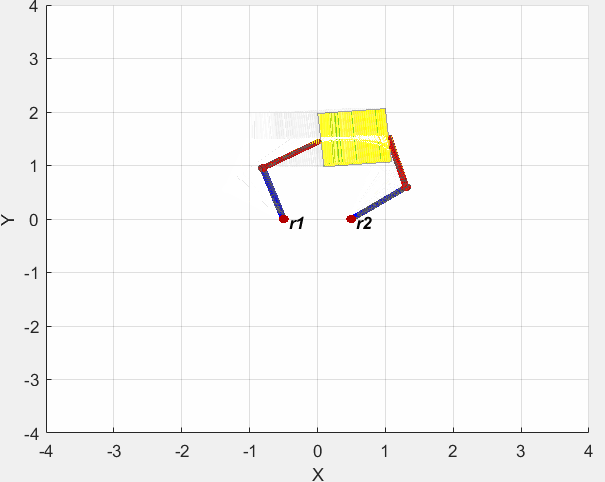
仿真结果如下图所示。

源代码

本文所需全部源代码已上传至我的GitHub，点击这里下载。运行two_link_object.m和two_link_distributed.m即可。使用前请确认RTB已经正确安装，下载和安装说明点击这里。

如果喜欢，欢迎点赞和fork。