问题描述

给定一个图(graph)，已知起始点 $S$ 和目标点 $G$ ，搜索图产生一条搜索树(search tree)，那么反向查找即可找到一条从起始点 $S$ 到目标点 $G$ 的路径。

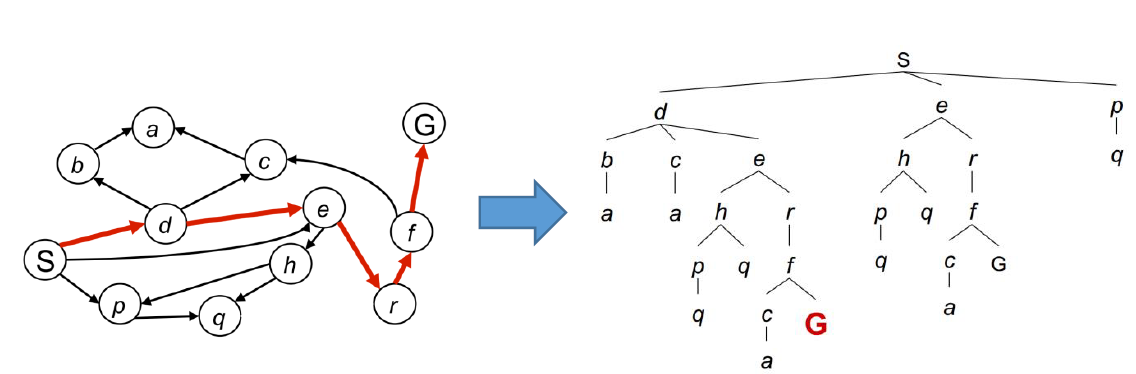
问题难点在于，如何构建这个搜索树？需要思考几个问题：

是否一定要构建一整个搜索树？如果不是，我们需要遍历哪些点？
搜索终止条件是什么？如果图是环形的怎么办？
如何尽快找到目标点 $G$ ？

为了解决这几个问题，我们提出容器(container)的概念。如果不需要遍历所有节点，那么只将需要遍历的点放入容器中，容器初始状态放入起始点 $S$ 。搜索终止条件就很明显了，当容器为空即终止。那么图是环形的怎么办呢？我们需要定义一个备忘录，标记以访问节点和未访问节点，避免重复搜索。

深度/广度优先搜索算法

深度优先搜索算法(depth first search)和广度优先搜索算法(breadth first search)用于解决构建搜索树问题的两种算法，他们的区别在于容器的不同。

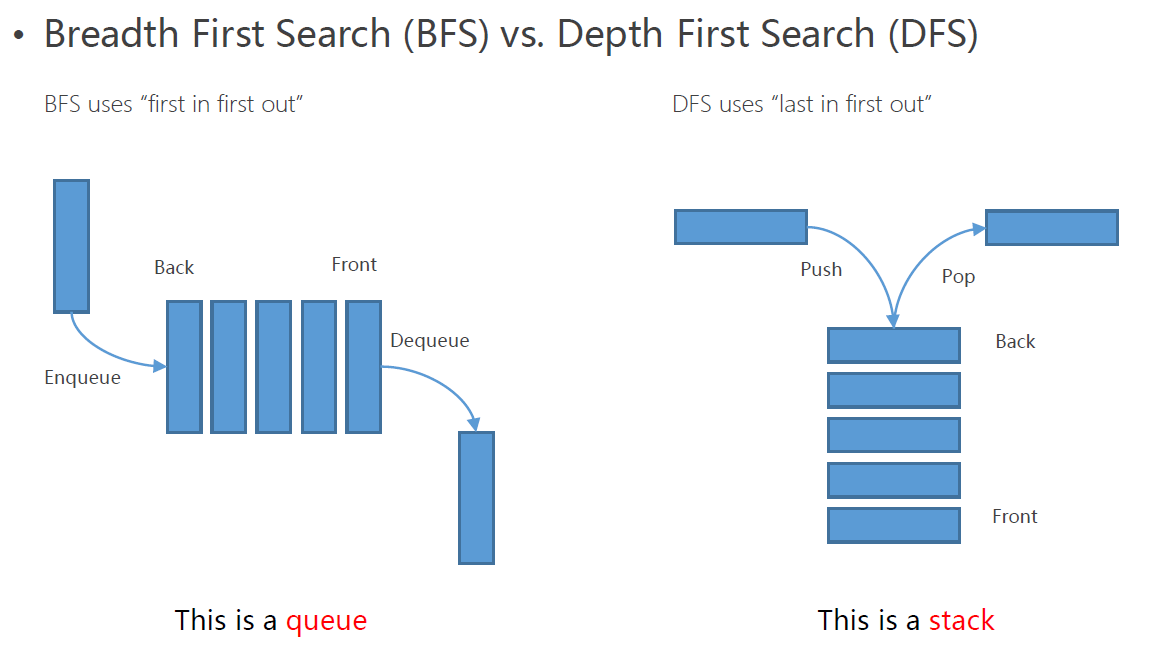
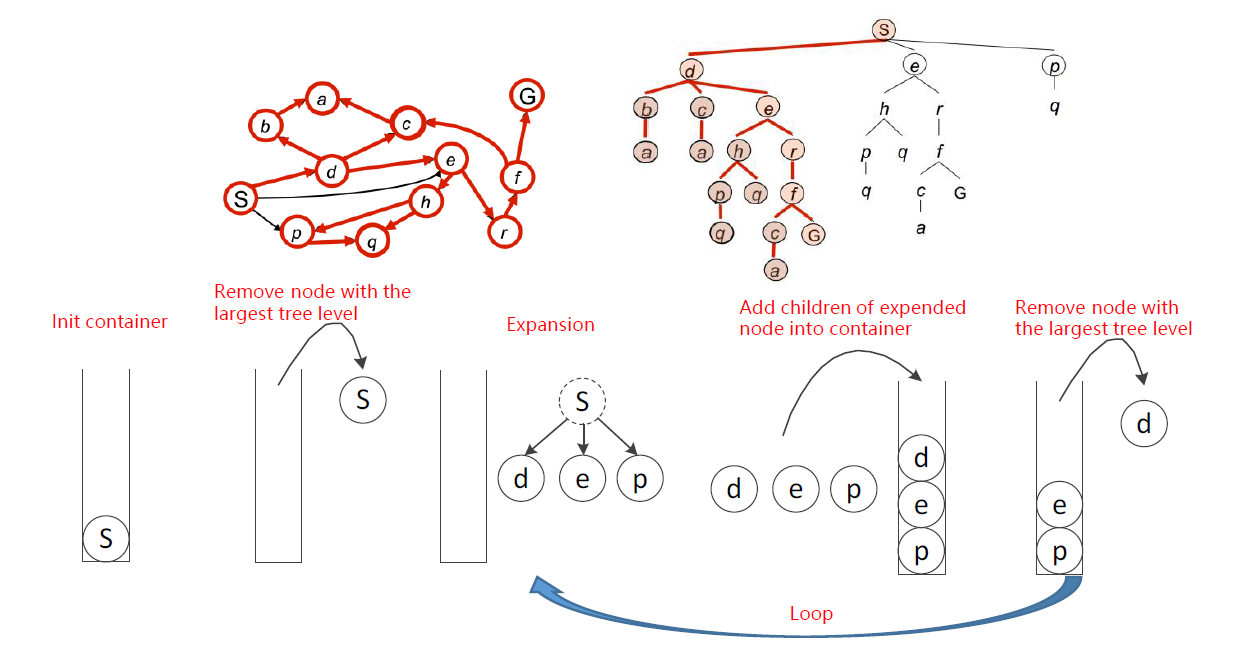
深度优先搜索算法的策略是：移除/扩展容器中最深的节点，即后入先出(last in first out)。

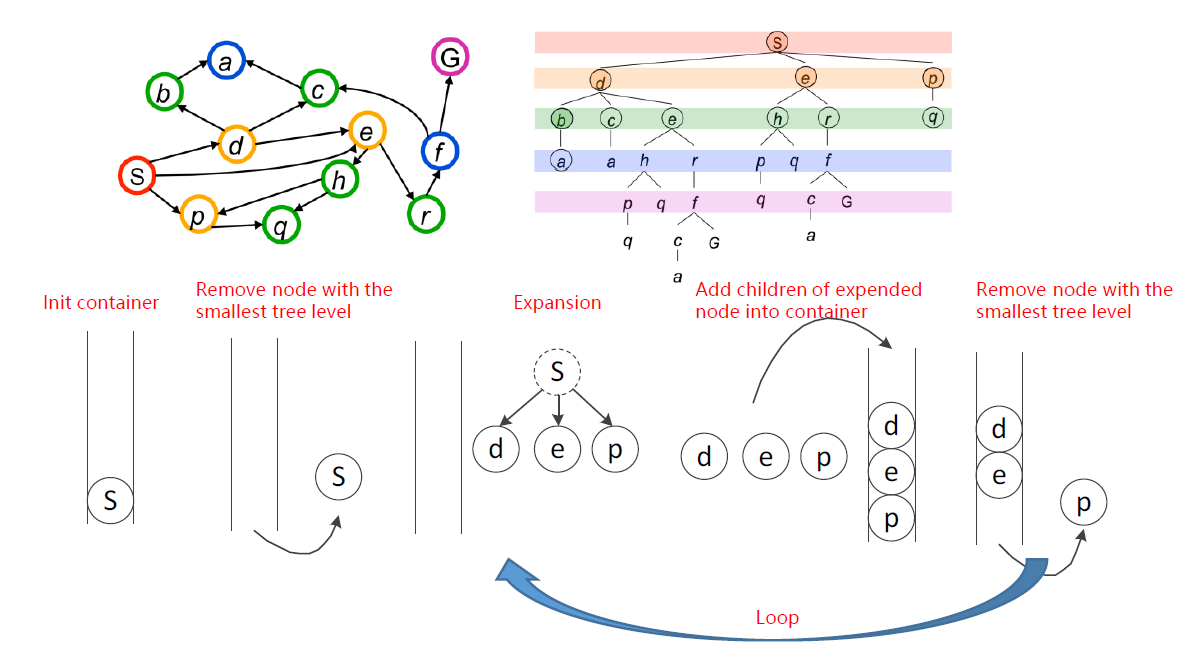
广度优先搜索算法的策略是：移除/扩展容器中最浅的节点，即先入先出(first in first out)。

两种算法标准模板

广度/深度优先搜索算法标准模板：

void bfs(邻接表, 起始节点, 目标节点)/*dfs(邻接表, 起始节点, 目标节点)*/{
    定义队列/*堆栈*/;
    定义备忘录，用于记录已经访问的节点;//如果图是树结构，则不需要备忘录
    将全部起始节点加入到队列/*堆栈*/中（空路径后加该节点）;
    更新备忘录；//必须加入时更新备忘录
    while (队列不为空){
        获取当前队列(当前层级)中的节点个数；//必须在这里读队列长度，因为后面队列长度会变
        for (该层所有节点){
            复制当前节点；
            出队/*出栈*/当前节点；
            for (全部目标节点){//最关键的循环终止条件
                if (当前节点==当前目标节点){
                    存当前路径；
                    继续/返回；//只需一条路径用返回，多条用继续
                }
            }
            for (邻接节点：邻接表[当前节点]){
                if (邻接节点可行且未访问过){
                    //如果入队时不更新备忘录，此时有可能又搜到上层节点
					加入该邻接节点到队列/*堆栈*/（当前路径后加该邻接节点）；
                    更新备忘录；
                }
            }
        }
    }
    遍历完毕，返回；
}

由于广度优先和深度优先仅取决于容器的不同，所以上面以广度优先搜索为基础，用注释符号标注出了深度优先不同于广度优先的地方。

注意：该标注模版仅能保证完全遍历，但搜索的路径是否满足要求需要具体分析。

797. 所有可能的路径（解法一）

接下来以力扣题797. 所有可能的路径为例，给出广度/深度优先搜索的题解。

给你一个有 n 个节点的 有向无环图（DAG），请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点，空就是没有下一个结点了。

译者注：有向图是有方向的，即规定了 a→b 你就不能从 b→a 。

以下实例为我手撕的面试题，可惜没当场撕出来。

该题指定了起始点为{0,3}，目标点为{7,8} ，输出{0,3}到{7,8}的所有路径。

输入实例：{{1,2},{5},{5},{4},{6},{7,8},{8},{},{}}

输出实例：{{0,1,5,7},{0,1,5,8},{0,2,5,7},{0,2,5,8},{3,4,6,8}}

0 3
/ \ |
1 2 4
\ / |
5 6
/ \ /
7 8

注意到该题为无环图，因此解法等同于层序遍历多叉森林，无需备忘录，而终止条件并非为了终止循环，而是为了记录路径。

//用于入队、入栈的节点结构
struct Node{
    int id;
    vector<int> path;
    
    Node(int id){
        this->id = id;
        this->path = {id};
    }
    
    Node(int id, vector<int> path){
        this->id = id;
        this->path = path;
        this->path.push_back(id);
    }
};
// 广度优先搜索
vector<vector<int>> bfs(vector<vector<int>> graph, vector<int> start, vector<int> goal){
    queue<Node> q;
    vector<vector<int>> results;
    int depth = 0;
    for (int s: start) q.push(Node(s));
    while (!q.empty()){
        int n = q.size();
        for (int i=0; i<n; i++){
            Node p = q.front();
            q.pop();
            for (int g: goal){
               if (p.id==g){
                    results.push_back(p.path);
                    continue;
                } 
            }
            for (int next: graph[p.id]){
                q.push(Node(next,p.path));
            }
        }
        depth++;
    }  
    return results;
}
// 深度优先搜索
vector<vector<int>> dfs(vector<vector<int>> graph, vector<int> start, vector<int> goal){
    stack<Node> q;//区别1
    vector<vector<int>> results;
    int step = 0;
    for (int s: start) q.push(Node(s));
    while (!q.empty()){
        int n = q.size();
        for (int i=0; i<n; i++){
            Node p = q.top();//区别2
            q.pop();
            for (int g: goal){
               if (p.id==g){
                    results.push_back(p.path);
                    continue;
                } 
            }
            for (int next: graph[p.id]){
                q.push(Node(next,p.path));
            }
        }
        step++;
    }  
    return results;
}
int main() {
    vector<vector<int>> graph = {{1,2},{5},{5},{4},{6},{7,8},{8},{},{}};
    vector<int> start = {0,3};
    vector<int> goal = {7,8};
    vector<vector<int>> paths;
    paths = bfs(graph,start,goal);
    // paths = dfs(graph,start,goal);
    return 0;
}

深度优先搜索的递归回溯算法

深度优先搜索算法也可以按照递归写，模板如下：

void dfs(当前节点){
    if (当前节点==目标节点){
        返回；//找到即返回
    }
    for (当前节点的所有下层节点){
        dfs(下层节点)；//对子树做dfs
    }
}
void main(){
    判断边界条件，是否能直接返回;
    dfs(起始节点)；
    遍历完毕，返回；    
}

通过上述模板，可以实现多叉森林中所有点的遍历，但是会出现重复遍历的现象。相当于搜的过程中发现此路不通，于是走了回头路。

那么问题来了，如果需要存路径，则必须删除这些回头路，怎么办？于是有了下面的回溯算法。

回溯算法

回溯算法(back tracking)也可以叫做回溯搜索法，它是一种搜索的方式。回溯是递归的副产品，只要有递归就会有回溯。

回溯算法的模板与上面深度优先搜索算法模板几乎完全一致，区别在于递归函数的前后分别有节点处理和撤销处理的两个操作。

回溯算法标准模板：

void backTracking(当前节点){
    if (当前节点==目标节点){
        存当前路径；
        返回；//找到即返回
    }
    for (当前节点的所有下层节点){
        当前节点加入路径；//节点处理
        backTracking(下层节点)；//对子树做bt
        路径中撤销当前节点；//撤销处理
    }
}
void main(){
    判断边界条件，是否能直接返回;
    backTracking(起始节点)；
    遍历完毕，返回；    
}

回溯算法中，for循环可以理解是横向遍历，backTracking（递归）就是纵向遍历，这样就把这棵树全遍历完了。

797. 所有可能的路径（解法二）

这里用深度优先递归回溯方法解决力扣题797. 所有可能的路径。

void dfsbt(vector<vector<int>>& paths, vector<int>& path, vector<vector<int>> graph, int start, int goal){
    if (start==goal){
        paths.push_back(path);
        return;
    }
    for (int next: graph[start]){
        path.push_back(next);
        dfsbt(paths,path,graph,next,goal);
        path.pop_back();//撤销处理
    }
}

int main() {
    vector<vector<int>> graph = {{1,2},{5},{5},{4},{6},{7,8},{8},{},{}};
    vector<int> start = {0,3};
    vector<int> goal = {7,8};
    vector<vector<int>> paths;
    // 与bfs每一个节点复制并维持一条路径不同，dfs有几条可行路径就维持几条
    for (int s: start){
        for (int g: goal){
            vector<int> path = {s};
            dfsbt(paths,path,graph,s,g);
        }
    }
    return 0;
}

Dijkstra算法

前面考虑的是有向无环无权图，bfs搜索中不会出现重复遍历，变量depth直接记录了路径的长度。

但是对于有向有环加权图，输出所有路径是不可能的，因为环的存在，每个节点能够重复遍历，所以路径有无数条。

为了解决环的问题，必须在bfs中引入备忘录，可以套用前面的模板，把bfs算法扩展到有向有环图上。

带备忘录的广度优先搜索算法

还是以力扣题797. 所有可能的路径为例，结合前面的模板，给出以下题解。

// 带备忘录的广度优先搜索
vector<vector<int>> bfsv(vector<vector<int>> graph, vector<int> start, vector<int> goal){
    queue<Node> q;
    vector<vector<int>> results;
    vector<int> visited(graph.size());//备忘录
    int depth = 0;
    for (int s: start) {
        q.push(Node(s));
        visited[s] = 1;//入队加备忘
    }
    while (!q.empty()){
        int n = q.size();
        cout<<depth<<" - ";
        for (int i=0; i<n; i++){
            Node p = q.front();
            q.pop();
            cout<<p.id<<" ";
            for (int g: goal){
               if (p.id==g){
                    results.push_back(p.path);
                    continue;
                } 
            }
            for (int next: graph[p.id]){
                if (!visited[next]){
                    q.push(Node(next,p.path));
                    visited[next] = 1;//入队加备忘
                }                
            }
        }
        depth++;
        cout<<endl;
    }  
    return results;
}
int main() {
    // [4,2,5,6,4]、[4,6,4]形成环
    vector<vector<int>> graph = {{1,2},{5},{5},{4},{2,6},{6,7,8},{4,8},{},{}};
    vector<int> start = {0,3};
    vector<int> goal = {7,8};
    cout<<"算法的遍历顺序："<<endl;
    vector<vector<int>> paths;
    paths = bfsv(graph,start,goal);
    cout<<"输出的路径："<<endl;
    for (auto p: paths) {
        for (int n: p) cout<<n<<" "; 
        cout<<endl;
    }
    return 0;
}

得到的输出如下：

算法的遍历顺序：
0 - 0 3 
1 - 1 2 4 
2 - 5 6 
3 - 7 8 
输出的路径：
0 1 5 7 
0 1 5 8

可以看出，对于有环图，在原有bfs算法引入备忘录可以保证将所有节点不重复的全部遍历一遍。

但是，由于备忘录的存在，节点无法重复遍历，输出的路径变少了。

Dijkstra算法模板

针对有向有环加权图，考虑边的权值，Dijkstra算法解决两点之间最小权值和的路径，即距离最短路径。

Dijkstra算法标准模板：

数组 dijkstra(邻接表, 起始节点, 目标节点){
    定义dp数组，记录起始节点到所有节点的距离，初始化为正无穷；
    dp[起始节点]=0；
    定义优先队列，按照距离由小到大排序;
    将[起始节点,起始节点距离(0)]加入到优先队列中;
    while (优先队列不为空){
        [当前节点,当前节点距离]=优先队列前端节点；
        出队优先队列前端节点；
        if (当前节点==目标节点){//循环终止条件（可选）
            返回当前节点距离；
        }
        if (当前节点距离>dp[当前节点]){//循环继续条件
             继续；
        }
        for (当前节点的所有邻居节点){
            邻居节点经过当前节点到初始节点的距离=dp[当前节点]+当前节点与邻居节点之间的边权值；
            if (dp[邻居节点]>邻居节点经过当前节点到初始节点的距离){
                //更新dp数组
                dp[邻居节点]=邻居节点经过当前节点到初始节点的距离;
                将[邻居节点，dp[邻居节点]]加入到优先队列中；
            }
        }
    }
    遍历完毕，返回dp数组；
}

743. 网络延迟时间

接下来以力扣题[743. 网络延迟时间为例，给出Dijkstra算法的题解。

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过有向边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

int networkDelayTime(vector<vector<int>> &times, int n, int k) {
    const int inf = INT_MAX / 2;
    //建图，得到邻接表
    vector<vector<pair<int, int>>> graph(n);
    for (auto &t : times) {
        int x = t[0] - 1, y = t[1] - 1;//-1是因为编号起始于1
        graph[x].emplace_back(t[2],y);//第一个是权值，第二个是邻居节点
    }
    // 记录最短路径的权重，你可以理解为 dp table
    vector<int> dist(n, inf);
    // base case，start 到 start 的最短距离就是 0
    dist[k - 1] = 0;
    // 优先级队列，distFromStart 较小的排在前面
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> q;
    // 从起点 start 开始进行 BFS
    q.emplace(0, k - 1);
    while (!q.empty()) {
        auto p = q.top();
        q.pop();
        int time = p.first, x = p.second;
        if (dist[x] < time) {
            // 已经有一条更短的路径到达 curNode 节点了
            continue;
        }
        // 将 curNode 的相邻节点装入队列
        for (auto &edge : graph[x]) {
            // 看看从 curNode 达到 nextNode 的距离是否会更短
            int y = edge.second, d = dist[x] + edge.first;
            if (d < dist[y]) {
                // 更新 dp table
                dist[y] = d;
                // 将这个节点以及距离放入队列
                q.emplace(d, y);
            }
        }
    }
    // max_element返回地址指针
    int ans = *max_element(dist.begin(), dist.end());
    return ans == inf ? -1 : ans;
}

star2dust

【力扣刷题】深度/广度优先搜索算法思路解析和标准模板