• 写在前面
• 如何仿真静态编队控制
  • 构建stress matrix
  • MATLAB求解LMI问题
  • 静态编队控制源代码
• 如何仿真时变轨迹和队形变换
  • 轨迹生成
  • 时变leader控制律
  • 时变轨迹和队形变换源代码

写在前面

原论文标题：Affine Formation Maneuver Control of Multiagent Systems.

之前的文章讲了赵世钰的仿射编队控制原理^[1]，进行了相关理论分析，发出来之后有不少同学私信问我如何复现他的论文。于是我现在再写这篇文章填个坑，把如何用MATLAB复现的思路讲一下，给之前的文章做个结尾。

如何仿真静态编队控制

读完赵的论文后，相信大家对控制算法已经掌握了，毕竟在形式上和一般的consensus极其相似。但是相比拉普拉斯矩阵，stress matrix的构建更加麻烦。下面详细讲一下在MATLAB中如何构建stress matrix。

我们首先给出一个任意的连通图，由关联矩阵$D$定义。

% incidence matrix
D = [1,-1,0,0,0,0,0,0,0,-1,0,1;
    -1,0,0,0,0,0,1,-1,0,0,0,0;
    0,1,-1,0,0,0,0,0,1,0,0,0;
    0,0,0,0,0,1,-1,0,0,1,-1,0;
    0,0,1,-1,0,0,0,0,0,0,1,-1;
    0,0,0,0,1,-1,0,0,-1,0,0,0;
    0,0,0,1,-1,0,0,1,0,0,0,0];
L = D*D';
H = D';

为了确定stress matrix $\Omega$，还需要再给出期望的队形位置$r$。为了简单起见，代码中r代表$P(r)$，P代表$\bar P(r)$。

%% dimensions
[n,m] = size(D);
d = 2;

% r represents P(r)
r = [2,0;
    1,1;
    1,-1;
    0,1;
    0,-1;
    -1,1;
    -1,-1];
    
% P represents \bar P(r)
P = [r,ones(n,1)];

构建stress matrix

接下来，我们按照论文VII-A的方法构建stress matrix $\Omega$。

第一步，创建$E$矩阵，使得$E\omega=0$，其中$\omega\in\mathbb R^m$为每条边对应的权重，各元素与$D$的列对应。

由于$\Omega=H^T\operatorname{diag}(\omega)H$和$\Omega \bar P(r)=0$，$\bar P^T(r)H^T\operatorname{diag}(\omega)H=\bar P^T(r)H^T\operatorname{diag}(\omega)[h_1,\cdots,h_n]=0$。因为$\operatorname{diag}(\omega)h_i=\operatorname{diag}(h_i)\omega$，所以$\bar P^T(r)H^T\operatorname{diag}(h_i)\omega=0,\forall i=1,\cdots,n$。

E = [];
for i=1:n 
    E = [E;P'*H'*diag(H(:,i))];
end

定义$Z=[z_1,\cdots,z_q]\in\operatorname{null}(E)$，则$\omega=Zc$，其中$c\in\mathbb R^q$是系数。

z = null(E);
c = zeros(size(z,2),1);

第二步，求系数$c$。对$\bar P(r)$奇异值分解，$\bar P(r)=U\Sigma V^T$。令$U=[U_1,U_2]$，其中$U_1$包含前$d+1$列。因为$\operatorname{rank}(\bar P(r))=d+1$，$U_1$为$\bar P(r)$的列空间，$U_2$为$\bar P^T(r)$的零空间，所以$U_1^T\Omega U_1=0$，$U_2^T\Omega U_2>0$。将$\omega=Zc$代入，$U_2^TH^T\operatorname{diag}(Zc)HU_2=\sum_{i=1}^q c_iU_2^TH^T\operatorname{diag}(z_i)HU_2>0$。

% svd
[U,S,V] = svd(P);
U1 = U(:,1:d+1);
U2 = U(:,d+2:end);
% calculate M
for i=1:size(z,2)
	M{i} = U2'*H'*diag(z(:,i))*H*U2;
end

令$M_i=U_2^TH^T\operatorname{diag}(z_i)HU_2$，则只需求解LMI问题：$\sum_{i=1}^q c_iM_i>0$。

MATLAB求解LMI问题

MATLAB求解LMI问题步骤如下：

• 初始化；

% Initialization
setlmis([]);

• 确定待定变量和不等式；

lmivar(type,struct)指定变量为未知变量，type=1表示变量为对称矩阵，struct=[1,0]表示只有1个block，且为scalar。

lmiterm(termid,A,B,flag)指定相应的不等式，termid=[-1,1,1,c(i)]，第一项表示第1个不等式，负号表示$>0$，第二、三项表示处于哪个位置，如(1,1)表示处于第1行第1列，第四项表示该不等式对应哪一个未知变量。这里令$c=[c_1,\cdots,c_q]$，不等式为$c_1M_1+\cdots+c_qM_q>0$。lmiterm定义每一个$c_iM_i$，不等式号为1，位置都为(1,1)。

for i=1:size(z,2)
	% Defining the Decision Variables
    c(i) = lmivar(1,[1,0]);
    % Define the LMIs one by one
    lmiterm([-1,1,1,c(i)],1,M{i});
end

• 建立模型和求解。

getlmis得到对应LMI问题模型，feasp求解LMI问题。

lmi = getlmis;
[~,csol] = feasp(lmi);
for i=1:size(null_E,2)
    c(i) = dec2mat(lmi,csol,c(i));
end
c = c/norm(c);
cM = [M{:}]*kron(c,eye(size(M{1},2)));
% check if cM>0

求解出$c$之后即可得到$\Omega=H^TZcH$。

w =  z*c;
Omega = H'*diag(w)*H;

静态编队控制源代码

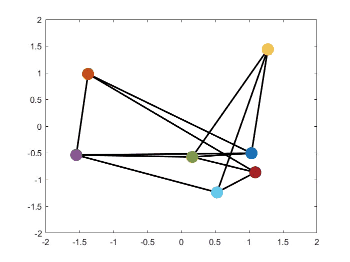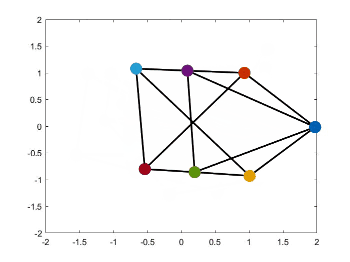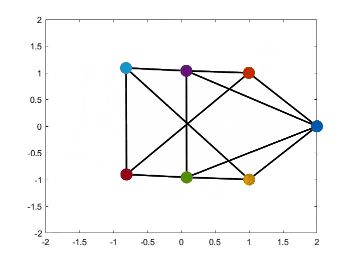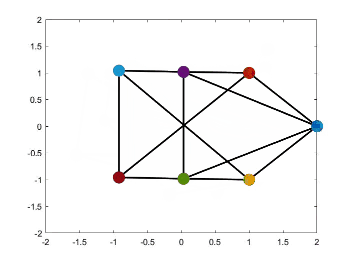
静态编队控制源代码见我的GitHub，见项目paper-simulation。运行Zhao2018Affine文件夹下的文件affine_formation.m，即可得到下面的仿真结果。

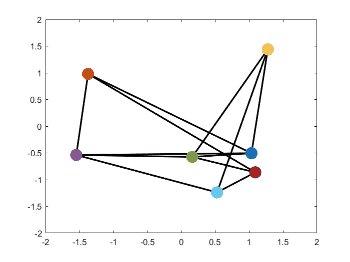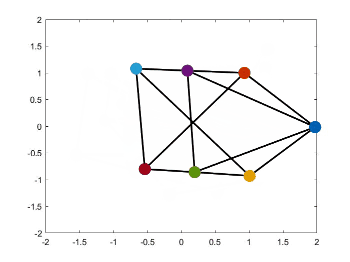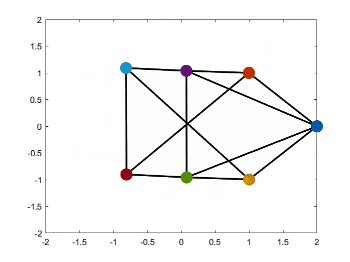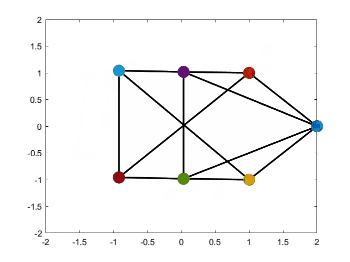
如何仿真时变轨迹和队形变换

时变队形有两个难点，一个是轨迹生成，另一个是时变leader控制律。

轨迹生成

轨迹生成部分我是对给定队形做仿射变换，即$x_r=Ar+b$。

$b$对应代码里的via，$A$对应代码里的T_1*T_2，要对$A,b$的每一个元素生成轨迹，最后再合并成$x_r$。

via = [0,0;
    5,0;
    10,0;
    10,-5;
    10,-10;
    5,-10;
    0,-10];
for j=1:size(via,1)
    if ~mod(j,2)
        if j==4
            T1 = diag([0.1,1]);
        else
            T1 = diag([1,0.1]);
        end
    else
        T1 = eye(2);
    end
    T2 = rot2(-pi/2*floor((j-1)/2));
    ra(:,:,j) = r*T2'*T1'+via(j,:);
    qvia(j,:) = [vec(T1*T2)',via(j,:)];
    for i=1:m
        plot(ra(edge(:,i),1,j),ra(edge(:,i),2,j),'k','linewidth',2); hold on
    end
end
[qr,dqr,ddqr,tr] = mstraj_(qvia,ones(1,6),0.1,0.2);
A = reshape(qr(1,1:4)',[2,2]);
b = qr(1,5:6)';
xr = r*A'+b';

时变leader控制律

写这个控制律其实不难，只是有点麻烦，不能像拉普拉斯矩阵一样写成矩阵形式，所以只能一条边一条边的求和。

gamma = diag(Omega);
% follower 4:n
for i=4:n
    err_sum = [0,0];
    edge_ind = find(D(i,:)~=0);
    for k=edge_ind
        node_ind = find(D(:,k)~=0);
        j = node_ind(node_ind~=i);
        err_sum = err_sum+z(k)*(x(i,:)-x(j,:)-dx(j,:));
    end
    dx(i,:) = -1/gamma(i)*err_sum;
end
% leader 1:3
dx(1:3,:) = dxr(1:3,:)-alpha*(x(1:3,:)-xr(1:3,:));

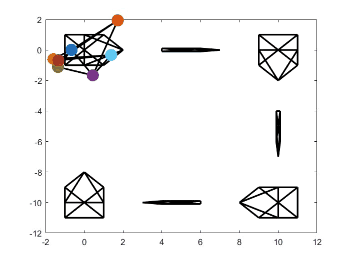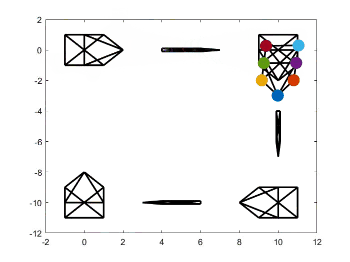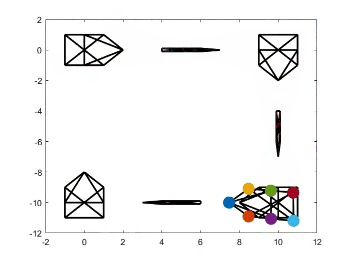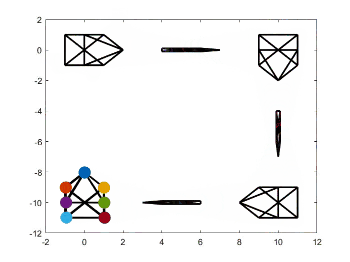
时变轨迹和队形变换源代码

时变轨迹和队形变换源代码见我的GitHub，见项目paper-simulation。运行Zhao2018Affine文件夹下的文件affine_maneuver.m，即可得到下面的仿真结果。