写在前面
本文使用的工具为MATLAB以及Peter Corke的RTB(Robotics Toolbox)。基于RTB 10.3.1版本,我写了RTE(Robotics Toolbox Extension),增加了一些移动机器人、机械臂以及路径规划相关代码。同时,RTE也修复了原RTB的一些小bug。
听说最近RTB出了10.4,不知道bug修复完没有,有用过的同学可以谈谈感想。个人建议这篇文章最好用我GitHub里的RTE工具箱,下载点这里。安装方法见README文件,写的很详细了。
本文的任务是利用MATLAB和RTB建模二连杆机械臂的动力学,并与MATLAB自带的simulink/simscape仿真进行对比,验证RTB建模的正确性。本文并不涉及控制部分,只是教大家如何建模真实的多刚体系统。
二连杆机械臂
如图1所示,我们要研究的是竖直平面上的二连杆机械臂,也可以说是双摆。因为本文不做控制,所以我们要模拟机械臂在重力的作用下运动的过程。
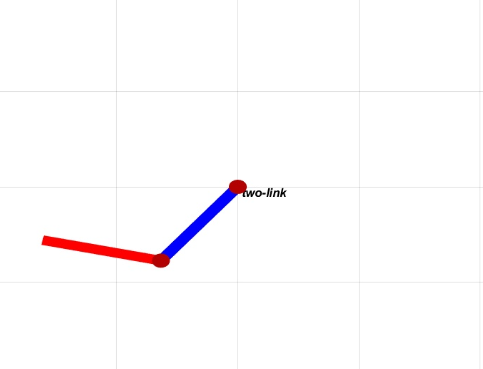
图1. 竖直平面上的二连杆机械臂
这里给出二连杆机械臂的动力学建模过程,之后可以代入数值验证代码正确性。
机械臂的动能为
T(θ,θ˙)=21m1∥v1∥2+21ω1TI1ω1+21m2∥v2∥2+21ω2TI2ω2,(1)
其中,I1,I2是关于质心的转动惯量。
分析各连杆关于质心的位置和速度为
xˉ1yˉ1xˉ2yˉ1=r1c1=r1s1=l1c1+r2c12=l1s1+r2s12xˉ1˙xˉ1˙xˉ2˙xˉ1˙=−r1s1θ˙1=r1c1θ˙1=−(l1s1+r2s12)θ˙1−r2s12θ˙2=(l1c1+r2c12)θ˙1+r2c12θ˙2
其中,r1,r2是关节离重心的距离。代入式1得,
T(θ,θ˙)=21[θ˙1θ˙2]T[α+2βc2δ+βc2δ+βc2δ][θ˙1θ˙2],
其中
αβδ=Iz1+Iz2+m1r12+m2(l12+r22)=m2l1r2=Iz2+m2r22。
参考我之前柔性机械臂建模的文章中的拉格朗日运动方程,可得
dtd∂θ˙∂T∂θ∂T=[α+2βc2δ+βc2δ+βc2δ][θ¨1θ¨2]+[−2βs2θ˙2−βs2θ˙2−βs2θ˙20][θ˙1θ˙2],=[0−(βs2θ˙12+βs2θ˙1θ˙2)]=[−βs2θ˙2−βs2(θ˙1+θ˙2)βs2θ˙10][θ˙1θ˙2]。
上面这第二步推导是真的难,我想了好久才想出来,这说明哥氏力其实表达方式不唯一。
两式相减得到
[α+2βc2δ+βc2δ+βc2δ][θ¨1θ¨2]+[−βs2θ˙2βs2θ˙1−βs2(θ˙1+θ˙2)0][θ˙1θ˙2]=[τ1τ2]
重力和摩擦力很简单,它们都只与θ相关,与θ˙无关,这里就省略了。
RTB建模
lx = 1; lr = 0.1; % 连杆的长度和半径
gy = 9.81; % 重力加速度(这里在y轴方向,因为z轴是关节转动轴)
fvis = 0; fcou = 0; % 粘性摩擦系数和库伦摩擦系数
- 建立连杆模型
这里的Cuboid和Cylinder都是我自己基于RTB写的类。
rod = Cuboid([lx,lr,lr]); % 建立成长方体
Irod = rod.inertia; % 可以直接获得转动惯量
这里建立成圆柱也行,获得转动惯量时需要进行一个刚体变换。
rod = Cylinder(lr,lx);
Rcyl = SO3.rpy([0 -pi/2 0]);
Irod = Rcyl.R*rod.inertia*Rcyl.R';
% 设定dh参数,质量,关节质心距离,关节约束,转动惯量,摩擦系数
dpm = {'a', lx, 'm', rod.mass, 'r', [-lx/2,0,0],...
'qlim', [-pi/2, pi/2],'I', Irod,...
'B', fvis, 'Tc', [fcou -fcou]};
% 建立二连杆机械臂,设定回转关节和重力
r = SerialLink([Revolute(dpm{:}),Revolute(dpm{:})],...
'name','two-link','gravity',[0 gy 0]);
经过以上步骤,二连杆机械臂建模完成,设置关节角qz,可以画出机械臂,效果如图1所示。
ws = [-4 4 -4 4 -4 4]; % 设置工作空间
plotopt = {'workspace', ws, 'nobase', 'notiles', 'noshading', 'noshadow', 'nowrist','top'}; % 设置绘图参数
h = r.plot(qz,plotopt{:});
仿真与验证
我们这里验证二连杆机械臂在重力作用下运动过程,即双摆实验。
% 给定初始关节角位置和速度
qz = zeros(1,2);
qd = zeros(1,2);
% 设定仿真时间10s
y0 = [qz,qd]'; tspan = [0 10];
% 刚体仿真用ode15s比较快,用accel函数直接获得关节加速度
tic
[tlist,ylist] = ode15s(@(t,y) [y(r.n+1:end);r.accel(y(1:r.n)',y(r.n+1:end)',zeros(1,r.n))],tspan,y0);
toc
% 差不多6s可出结果,然后画出机械臂即可
ws = [-4 4 -4 4 -4 4];
plotopt = {'workspace', ws, 'nobase', 'notiles', 'noshading', 'noshadow', 'nowrist','top'};
h = r.plot(ylist(:,1:r.n),plotopt{:});
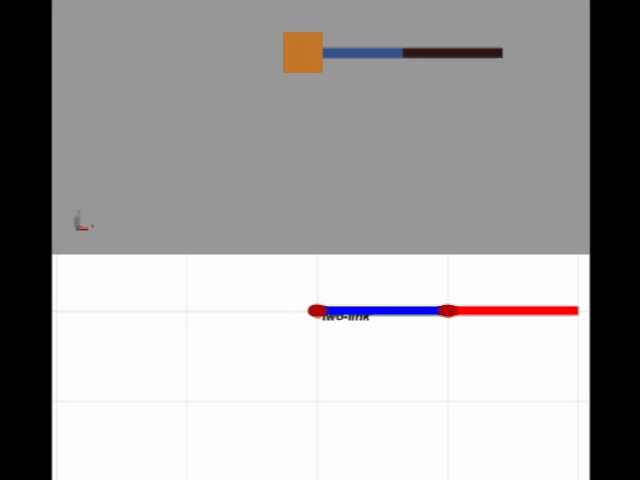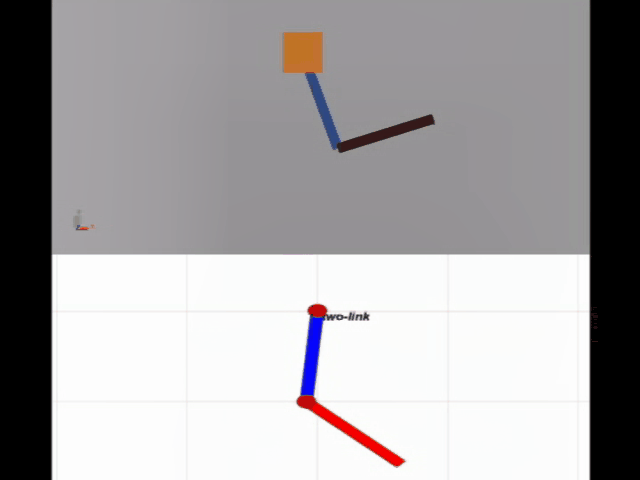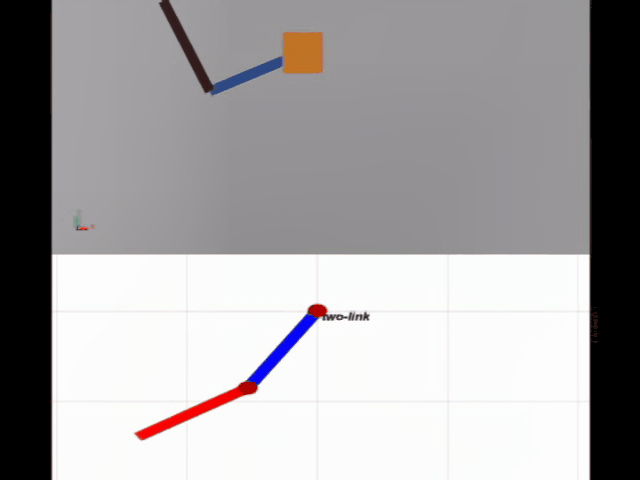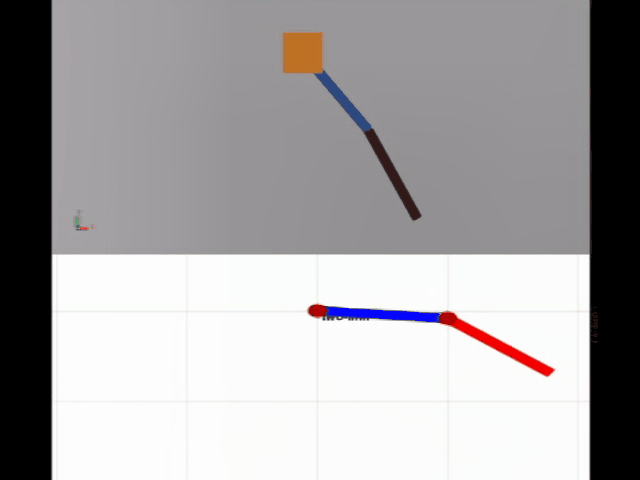
实验结果如下图所示。
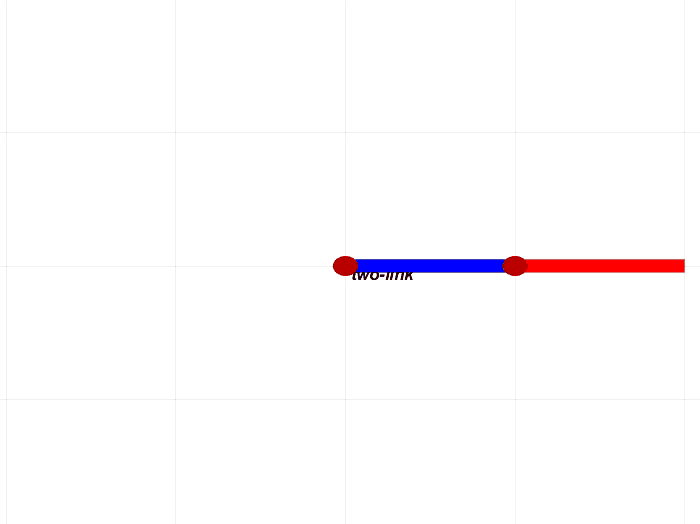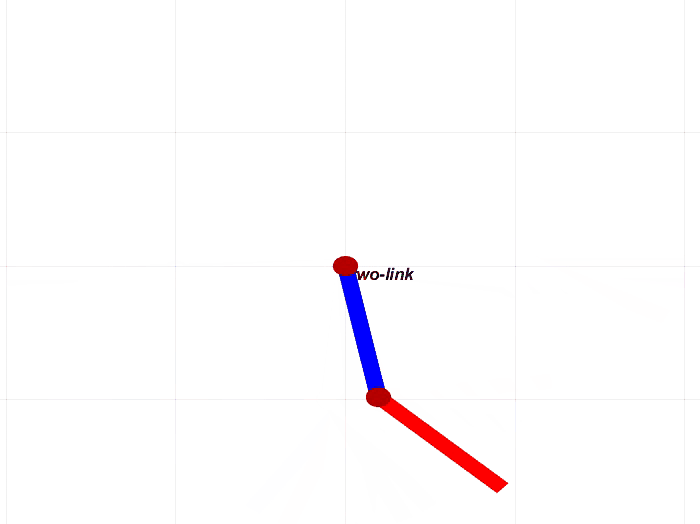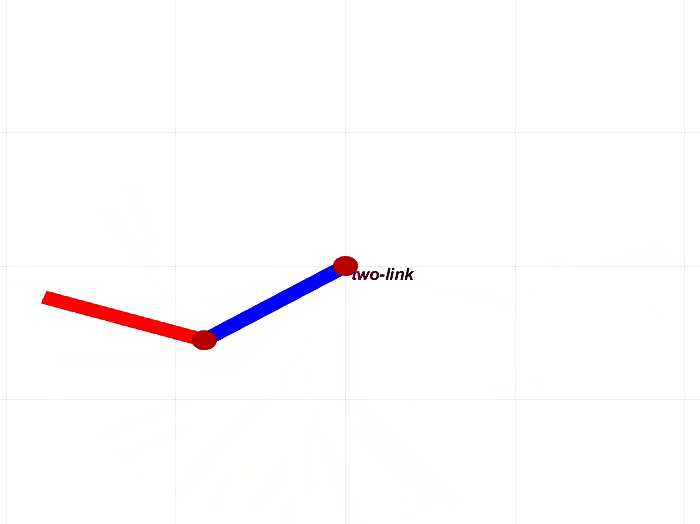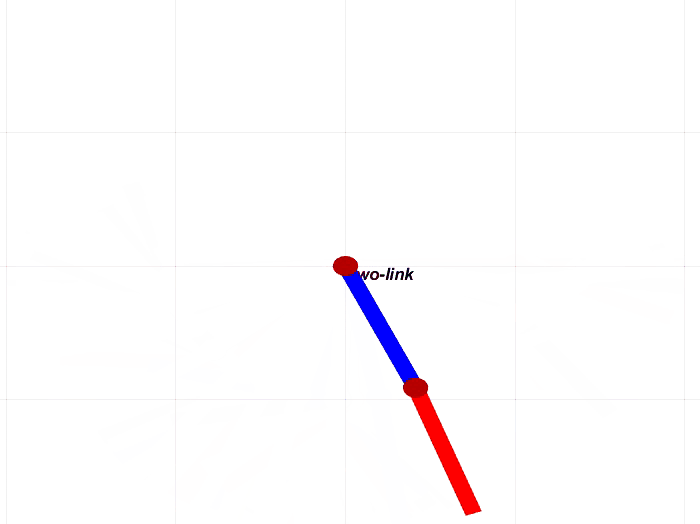
下面进行simulink/simscape的双摆仿真,对比实验如下图所示,可以看到前面几乎是同步的。
如何使用simscape搭建一个双摆系统,可以参考b站这个视频。
源代码
本文所需全部源代码已上传至我的GitHub,点击这里下载。运行two_link_test.m即可。使用前请确认RTB已经正确安装,下载和安装说明点击这里。
使用simulink/simscape做的双摆仿真也在该仓库里,见link_test.slx,但是需要MATLAB里有simscape的工具箱,否则打不开。另外MATLAB版本最好在2018b以上。
如果喜欢,欢迎点赞和fork。



