• 写在前面
• 一致性算法
  • 连续时间
  • 离散时间
• 一致性证明
  • 连续时间
  • 离散时间
• 矩阵理论
  • 特征值和特征向量
  • 特征多项式
  • 代数重数
  • 几何重数
• 总结

写在前面

最近在看一些分布式优化的文章，但是大部分文章都是用的离散时间算法。我之前一直研究的是连续时间一致性(consensus)控制问题，现在想把离散时间控制拾起来。

这篇文章前半部分讲解连续和离散系统的一致性算法，互相做个对比，加深一下印象和理解；后半部分回顾在算法证明中会用到的矩阵理论的基本知识。

下面进入文艺复兴环节，让我们回顾一下最经典的一致性算法和矩阵理论的基本知识吧。

一致性算法

考虑状态$x_i\in\mathbb R^m$，图$\mathcal G=(\mathcal V,\mathcal E)$和单积分器系统

$\dot x_i=u_i,\quad i\in\mathcal V.$

连续时间

首先，给出连续时间一致性算法：

$\dot x_i=-\sum_{j\in\mathcal N_i}a_{ij}(x_i-x_j),\quad i\in\mathcal V,$

写成矩阵形式为

$\dot x=-(L\otimes I_m)x,$

其中$A=[a_{ij}]\in\mathbb R^{n\times n}$是邻接矩阵(adjacency matrix)，如果$(j,i)\in\mathcal E$，那么$a_{ij}>0$，否则$a_{ij}=0$；$L=[l_{ij}]\in\mathbb R^{n\times n}$是拉普拉斯矩阵(Laplacian matrix)，满足

$l_{ii}=\sum_{j=1,j\neq i}^n a_{ij},\qquad l_{ij}=-a_{ij},\,i\neq j。$

离散时间

然后，给出离散时间一致性算法：

$x_{i,k+1}=\sum_{j\in\mathcal N_i}d_{ij}x_{i,k},\quad i\in\mathcal V,$

写成矩阵形式为

$x_{k+1}=(D\otimes I_m)x_{k},$

其中$k\in N$是离散时间指数(discrete-time index)；$D=[d_{ij}]\in\mathbb R^{n\times n}$是行随机矩阵(row-stochastic matrix)，满足$d_{ii}> 0$对所有$i\in\mathcal V$成立，如果$(j,i)\in\mathcal E$，那么$d_{ij}>0$，否则$d_{ij}=0$。

Vicsek模型^[1]是离散时间一致性算法的特例，该模型中如果$(j,i)\in\mathcal E$，那么令$d_{ij}=\frac{1}{1+|\mathcal N_i|}$，$|\mathcal N_i|$表示智能体$i$的邻居(neighbor)个数。但是Vicsek模型不一定能保证为双随机矩阵(doubly-stochastic matrix)。已知$L$的情况下，令$D=e^{-L}$虽然可以得到双随机矩阵，但是无法保证分布式实现。

想要得到满足前面条件的双随机矩阵，一种简单的办法是：如果$(j,i)\in\mathcal E$，那么令$d_{ij}=1/g$，$d_{ii}=1-\sum_{j\neq i} d_{ij}$，其中$g>n$。

一致性证明

无论对于连续时间或是离散时间系统，状态$x$都可以写成关于$t$或$k$的函数，即

$x(t)=(e^{-Lt}\otimes I_m)x(0)，$

或者

$x_k=(D^k\otimes I_m)x_0。$

下面需要一致集$\mathcal S=\{x\in\mathbb R^{nm}| x_1=\cdots=x_n \}$是吸引(attractive)的正不变(positive invariant)集，即满足

$\lim_{t\to\infty} e^{-Lt}=\lim_{k\to\infty}D^k=1_nc^T，$

才有$\lim_{t\to\infty} x(t)=\lim_{k\to\infty} x_k=(1_nc^T\otimes I_m)x(0)$。

连续时间

定理1 (Lemma 2.6 ^[2])：拉普拉斯矩阵$L\in\mathbb R^{n\times n}$对应的$e^{-Lt}, \forall t\geq 0$是主对角元大于0的行随机矩阵。另外，$\operatorname{Rank}(L)=n-1$当且仅当$L$有单个0特征根。此外，若$L$有单个0特征根，且$L^T$关于0特征根的标准化特征向量为$c$，即

$1_n^Tc = 1,\quad L^Tc = 0,$

那么$e^{-Lt}\to 1_nc^T$，当$t\to \infty$。

证明：由于$L$是方阵，将$-L$特征分解(谱分解)得到$-L=PJP^{-1}$，其中$P=[p_1,\cdots,p_n]\in\mathbb R^{n\times n}$，$J=\operatorname{diag}(0,-\lambda_2,\cdots,-\lambda_n)$。不失一般性，我们令$p_1=1_n$对应0特征根，而$\lambda_2,\cdots,\lambda_n$都大于0。

由矩阵指数的性质^[3]，易知$e^{-Lt}=Pe^{Jt}P^{-1}$。故$e^{-Lt}$有特征根1对应特征向量$1_n$，即$e^{-Lt}1_n=1_n$，因此是行随机矩阵。此外，可以看出$e^{Jt}\to \operatorname{diag}(1,0,\cdots,0)$，当$t\to\infty$，即

$Pe^{Jt}P^{-1}\to\begin{bmatrix}1_n &p_2&\cdots&p_n\end{bmatrix}\begin{bmatrix}1&0&\cdots &0\\ 0&0&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\ 0&0&\cdots&0\\ \end{bmatrix}\begin{bmatrix}c^T\\\nu_2^T\\\vdots\\ \nu_n^T \end{bmatrix},$

当$t\to\infty$。故$e^{-Lt}\to 1_nc^T$，当$t\to\infty$，又因为$e^{-Lt}$行随机，即$e^{-Lt}1_n=1_n(c^T1_n)=1_n$，故$1_n^Tc=1$。

引理1 (Lemma C.2)：给定矩阵$A\in\mathbb R^{n\times n}$和特征根$\lambda \in\mathbb C$，假设$x,y$满足(i)$Ax=\lambda x$，(ii)$A^Ty=\lambda y$，(iii)$x^Ty =1$。如果$|\lambda|=\rho(A)>0$，其中$\rho(A)$为$A$的谱半径，且$\lambda$是唯一具有最大模数(maximum modulus)的特征根，那么$\lim_{m\to\infty}(\lambda^{-1}A)^m\to xy^T$。

$A\in\mathbb R^{n\times n}$是可约矩阵(reducible)，即要么为全0矩阵，要么存在置换矩阵$P\in\mathbb R^{n\times n}$使得$P^TAP$为分块上三角阵(block upper triangular form)。 $A\in\mathbb R^{n\times n}$是非负矩阵(nonnegative)，即所有元素都大于等于0。

命题1 (Lemma C.3)：方阵$A\in\mathbb R^{n\times n}$是不可约的当且仅当与矩阵$A$对应的有向图$\Gamma(A)$是强连通的。

引理2 (Lemma C.4)：如果$A\in\mathbb R^{n\times n}$是非负的不可约(irreducible)矩阵，那么$\rho(A)$是$A$的一个特征根，且存在一个非0特征向量$x\geq 0$(即非负)使得$Ax=\rho(A)x$。

接下来需要证明$c\geq 0$且$c$是$L$关于0的左特征向量，即$L^T c=0$。由引理1和引理3可得，$c$是$(e^{-L})^T$的关于1的特征向量，再由下章的定理1.1，$c$是$L^T$关于0的特征向量。由引理2可知，$c\geq 0$。$L$是不可约矩阵可由强连通性保证，下面的引理3证明$L$的单个0特征根性质。

一般来说，$L$有至少一个0特征根，而圆盘定理(Gershgorin's disc theorem)只能确保$L$的根都位于右半平面或虚轴上，但无法保证0特征根只有一个。事实上，当图$\mathcal G$不连通时，可能有多个0特征根，且0特征根的个数等于图的连通分量个数。

引理3 (Lemma 2.4)：给定矩阵$A\in\mathbb R^{n\times n}$，其中$a_{ii}\leq 0$，$a_{ij}\geq 0$，$\forall i\neq j$，且$\sum_{j=1}^n a_{ij}=0$对任意$i$成立，那么$A$有至少一个0特征根和相关的特征向量$1_n$，其他非0特征根都位于右半开平面。此外，$A$有唯一的0特征根，当且仅当$A$对应的有向图$\Gamma(A)$有一个有向生成树(directed spanning tree)。

离散时间

引理4 (Lemma 2.16)：如果一个非负矩阵$A=[a_{ij}]\in\mathbb R^n$满足$\sum_{j=1}^nd_{ij}=\mu>0$，那么$\mu$是$A$关于特征向量$1_n$的一个特征根，且$\rho(A)=\mu$，其中$\rho(\cdot)$表示谱半径。另外，特征根$\mu$的代数重数(algebraic multiplicity)为1，当且仅当$A$对应的有向图$\Gamma(A)$有一个有向生成树。此外，如果$d_{ii}>0,i=1,\cdots,n$，(i) 那么$|\lambda|<\mu$对任意$\lambda\neq \mu$成立，(ii) 如果有向图$\Gamma(A)$有一个有向生成树，那么$\mu$是唯一具有最大模数的特征根。

证明：矩阵$A$行和为$\mu$，即$A1_n=\mu 1_n$。再由非负性和圆盘定理，$\rho(A)\leq \mu$。故$\mu$是$A$关于特征向量$1_n$的一个特征根，且$\rho(A)=\mu$。

(充分性) 若$A$对应的有向图$\Gamma(A)$有一个有向生成树，令$B=A-\mu I$，则$B$满足引理3的条件。$B$的0根的代数重数为1，自然$A$的$\mu$根代数重数也为1。

(必要性) (逆否) 若$A$对应的有向图$\Gamma(A)$没有向生成树，令$B=A-\mu I$，则$B$有不止一个0根，$A$的$\mu$根代数重数大于1。

定理2 (Perron-Frobenius theorem)：如果$A\in\mathbb R^{n\times n}$非负且不可约，那么 (i) $\rho(A)>0$，(ii) $\rho(A)$是$A$的一个特征根，(iii) 存在正向量$x$使得$Ax=\rho(A)x$，(iv) $\rho(A)$是$A$的一个代数重数为1(几何重数也为1)的特征根。

一个行随机矩阵$A$是不可分解且非周期的(indecomposable and aperiodic, SIA)，如果$\lim_{k\to \infty}A^k=1_n\nu^T$，即极限存在且每一行都相同。

定理3 (Lemma 2.19)：给定行随机矩阵$A\in\mathbb R^{n\times n}$。如果$A$有代数重数为1的特征根$\lambda=1$，且其他特征根满足$|\lambda|<1$，那么$A$是SIA。特别地，$\lim_{m\to\infty}A^m\to 1_n\nu^T$，其中$A^T\nu=\nu$且$1_n^T\nu=1$。此外，$\nu$的每一个元素非负。

证明：SIA和左特征向量可由引理1直接推出。而$A$和$A^T$特征根相同(下章的结论2.1)，由引理2可知特征根1对应的特征向量非负。

矩阵理论

主要介绍了特征值、特征向量、特征多项式、代数重数、几何重数以及重要的性质^[4][5]。

特征值和特征向量

这个定理前面有用到，如果0是$L$的一个特征根，那么$e^0=1$也是$e^{-L}$的一个特征根，且它们相应的特征向量都为$1_n$，反之也一样。

定义$\sigma (A)$为矩阵$A$的特征根集。有几个重要性质：

$n$ 阶方阵$A$是非奇异方阵的充要条件是$A$可逆，即可逆方阵就是非奇异方阵。以下命题等价：

• 一个矩阵非奇异当且仅当它的行列式不为零。
• 一个矩阵非奇异当且仅当它代表的线性变换是个自同构。
• 一个矩阵半正定当且仅当它的每个特征值大于或等于零。
• 一个矩阵正定当且仅当它的每个特征值都大于零。
• 一个矩阵非奇异当且仅当它的秩为$n$（满秩）。

证明：如果$λ∈σ(A)$，则存在一个非零向量$x$，使得$Ax=λx$，从而$(A+μI)x=Ax+μx=λx+μx=(λ+μ)x$。于是$λ+μ∈σ(A+μI)$。反过来，如果$λ+μ∈σ(A+μI)$，则存在非零向量$y$，使得$Ay+μy=(A+μI)y=(λ+μ)y=λy+μy$。于是$Ay=λy$, 从而$λ∈σ(A)$。

特征多项式

证明：

1. 多项式次数最高的两项和常数项已经给出，而其他求和项包含非对角因子$-a_{ij}$，故次数不会大于$n-2$，因为$t-a_{ij}$和$t-a_{jj}$不是因子。
2. $p_A(λ)=0⇔\operatorname{det}(λI−A)=0⇔(λI−A)x=0,x≠0⇔λ∈σ(A)$
3. 次数为$n⩾1$的多项式至多有$n$个不同零点。

$p_A(t)$的零点之和是$A$的迹$\operatorname{tr}(A)$，而零点之积则是$A$的行列式$\operatorname{det}(A)$。

代数重数

$λ$的代数重数是特征方程里面有几个根是$λ$。

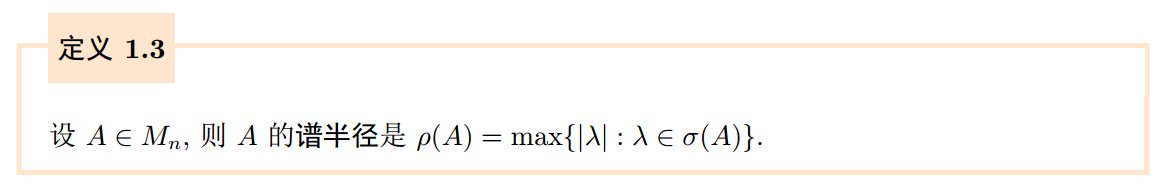
矩阵的谱半径(spectral radius)是模最大特征根对应的模数。

上述定理表明，一个奇异的复矩阵总可以稍加平移使之成为非奇异的。

几何重数

证明：由于$\operatorname{det}(tI−A^T)=\operatorname{det}(tI−A)^T=\operatorname{det}(tI−A)$, 我们有$p_{A^T}(t)=p_A(t)$, 所以有$p_A^T(λ)=0$ 当且仅当 $p_A(λ)=0$。 类似地，$\operatorname{det}(\bar tI−A^∗)=\operatorname{det}[(tI−A)^∗]=\overline{\operatorname{det}(tI−A)}$, 所以$p_{A^∗}(\bar t)=\overline {p_A(t)}$, 又$p_A^∗(\bar λ)=0$当且仅当$p_A(λ)=0$。

如果$x,y∈\mathbb C^n$两者都是$A∈M^n$的与特征值$λ$相伴的特征向量，那么$x$与$y$的任何非零的线性组合也是它的与$\lambda$相伴的特征向量 。实际上，与一个给定的$λ∈σ(A)$相伴的所有特征向量组成的集合与零向量合起来作成$\mathbb C^n$的一个子空间，该子空间就是$A−λI$的零空间，就是齐次线性方程组$(A−λI)x=0$的解集，由秩的关系知其维数是 $n−\operatorname{rank}(A−λI)$。该空间有个名字就是特征空间，下面给出特征空间的完整定义：

介绍完特征空间，就可以定义几何重数了，特征空间的维数即为几何重数。

可以证明特征值的几何重数小于或者等于它的代数重数的。

即，几何重数$=n-\operatorname{rank}(A-\lambda I)\leq k=$代数重数。

一个矩阵可对角化，当且仅当它是无亏的；它有完全不同的特征值，当且仅当它是无损的且是无亏的。考虑以下矩阵的特征值$λ=1$, 矩阵$\begin{bmatrix}1&0\\ 0&2\end{bmatrix}$，代数重数等于它的几何重数且都是 1, 它是无亏的，单位矩阵$I_2$是无亏的且是有损的，矩阵$\begin{bmatrix}1&1\\ 0&1\end{bmatrix}$，几何重数是1, 代数重数是2，它是有亏的且是无损的。

尽管$A$与$A^T$有相同的特征值，它们与给定特征值相伴的特征空间有可能是不同的。比如，矩阵$A=\begin{bmatrix}2&3\\ 0&4\end{bmatrix}$，那么$A$的与特征值2相伴的（一维）特征空间是由$\begin{bmatrix}1\\ 0\end{bmatrix}$生成的，而$A^T$的与特征值2相伴的特征空间是由$\begin{bmatrix}1&0\\ 0&-3/2\end{bmatrix}$生成的。

总结

• $λ$的代数重数是特征方程里面有几个根是$λ$。
• $λ$的几何重数是线性空间$Ax=λx$的维数。
• 代数重数大于等于几何重数，代数重数如果大于几何重数，那么原因在于这个矩阵的Jordan标准型里面有维数大于1的Jordan块。
• 强连通$\Leftrightarrow$有向生成树$\Leftrightarrow$不可约$\Leftrightarrow$最大模数特征根代数重数为1$\Leftrightarrow$相应特征向量非负
• 如果是行随机(行和为1)，则上面条件$\Leftrightarrow$SIA$\Leftrightarrow$极限为$1_n\nu^T$，其中$\nu$为左特征向量

---

1. Vicsek, T., Czirók, A., Ben-Jacob, E., Cohen, I., Shochet, O. (1995). Novel type of phase transition in a system of self-driven particles. Physical review letters, 75(6), 1226. ↩︎

2. Ren, W., & Beard, R. W. (2008). Distributed consensus in multi-vehicle cooperative control . London: Springer London. ↩︎

3. 矩阵指数. (2020, September 15). Retrieved from 维基百科, 自由的百科全书: https://zh.wikipedia.org/w/index.php?title=%E7%9F%A9%E9%98%B5%E6%8C%87%E6%95%B0&oldid=61692808 ↩︎

4. 特征值和特征向量. 小鱼吻水. https://www.cnblogs.com/zhoukui/p/7672972.html ↩︎

5. 特征多项式、代数重数与几何重数. 小鱼吻水. https://www.cnblogs.com/zhoukui/p/7685318.html ↩︎