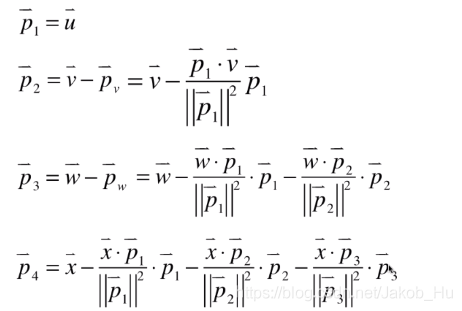• 写在前面
• 正交基与投影
• 高维投影和Gram-Schmidt过程
  • 三维空间
  • 四维及以上空间
• Gram-Schmidt过程构造标准正交基
• 后记
  • Section 4.1中的应用
  • Section 5.2中的应用
• 题外话
  • 两个定理
  • 微分方程求解

写在前面

原论文标题：Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication.

之所以想要写这篇文章，是因为最近在看的一篇分布式优化论文(Kia 2015)^[1]，其中有这么一个问题。

令$\Pi_n=I_n-\frac{1}{n}1_n 1_n^T$。为了简便表示，可以定义$r\in\mathbb R^n$和$R\in\mathbb R^{n\times (n-1)}$，且满足以下条件：

$r=\frac{1}{\sqrt{n}} 1_n，\,r^TR= 0，\,R^TR=I_{n-1}，\,RR^T=\Pi_n。$

那么如何得到期望的$R$？

显然这里，$[r, R]$是$n$维空间的一组标准正交基(orthonormal basis)。现在已知$r$需要求出所有$R$的列向量。这就需要线性代数中标准正交基和投影的知识。

正交基与投影

一个$n$维空间中任何一组线性无关(linearly independent)的向量，都是这个$n$维空间的一组基。当这组基的向量两两垂直(即$e_i^Te_j=0$)，则称为正交基(orthogonal basis)。而标准正交基只是将正交基又添加了一个条件，模长为1(即$\|e_i\|=1$)。一个空间可以有无数组基向量，正交基和标准正交基也同样是有无数组的。

一维投影相当于把一个向量投影到另一个向量，可以进一步求取正交基。以下图片来自Jakob_Hu的博客^[2]。

已知向量$u$和$v$，按照如上图所示方法可以求取投影$p=\frac{u^Tv}{\|u\|^2}u$。求出$p$后，进一步求出正交向量$v-p$非常容易。这就解决了在二维空间中求取一组正交基的问题，正交基为$p$和$v-p$。

高维投影和Gram-Schmidt过程

为了解决第一节提到的问题，我们需要一个能够通过任意维度的一组基构造空间的正交基的算法。

三维空间

以三维向量为例，假设存在一组三维向量，需要求出这三个向量所在空间的正交基，其中两个已经处理得到相互正交的向量$p_1$、$p_2$。再加上向量$w$构成三维空间的一组基。

下一步我们需要做$w$向$p_1$、$p_2$构成的二维子空间的投影$p$，则$w-p$即我们想要的正交向量。

1. 分别做$w$向$p_1$、$p_2$上的投影，得到$\frac{w^Tp_1}{\|p_1\|^2}p_1$和$\frac{w^Tp_2}{\|p_2\|^2}p_2$，则$p=\frac{w^Tp_1}{\|p_1\|^2}p_1+\frac{w^Tp_2}{\|p_2\|^2}p_2$；
2. 计算$w-p$，得到$w-\frac{w^Tp_1}{\|p_1\|^2}p_1-\frac{w^Tp_2}{\|p_2\|^2}p_2$即第三维的正交向量。

三维空间求正交基的整个过程可以看做是先求出相应的二维空间的正交基，进一步求取三维空间正交基。

四维及以上空间

与三维空间相似，先求取低维度空间的正交基，在其基础上进行高一维度正交基的求取。

给出任何一组$n$维空间的基，正交基的过程都可以通过逐一维度的计算得到。任何一个维度的向量都减去它在低维度空间中已经正交的向量的投影，这一过程就是Gram-Schmidt过程。

Gram-Schmidt过程构造标准正交基

回到第一节提到的问题，现在我们已知$n$维空间的任意一个向量$r$，如何利用Gram-Schmidt过程构造一组标准正交基。

% 维度为4
n = 4;
r = ones(n,1)/n;

% r'的零空间
N = @(A) eye(size(A,2))-pinv(A)*A;
R1 = N(r');
R1 = R1./vecnorm(R1);

% [r R1(:,1)]'的零空间
R2 = N([r R1(:,1)]');
R2 = R2./vecnorm(R2);

% [r R1(:,1) R2(:,2)]'的零空间
R3 = N([r R1(:,1) R2(:,2)]');
R3 = R3./vecnorm(R3);
R = [R1(:,1) R2(:,2) R3(:,3)];

由此构建第一节需要的$R$。

后记

这里最后提一下，按照前面这样定义的$R$会有什么好的性质。

首先，自不必说，有，

$r=\frac{1}{\sqrt{n}}\boldsymbol 1_n，\,r^TR=\boldsymbol 0，\,R^TR=I_{n-1}，\,RR^T=\Pi_n。$

然后，$P=[r,R]$显然是标准正交基组成的矩阵。由于$P$满秩，所以

$P^TP=PP^T=I_n，\,R^TP=[0_{n-1},I_{n-1}]，\, \Pi_n P=RR^TP=R[0_{n-1},I_{n-1}]=[0_{n-1},R]。$

下面给出该性质在第一节所看论文中的应用。

Section 4.1中的应用

定义图$\mathcal G$是强连通平衡图，其拉普拉斯矩阵为$L$。现有动力学如下

$\begin{aligned} \dot v&=\alpha\beta Lx，\\ \dot x&=-\alpha\nabla f(x)-\beta Lx-v， \end{aligned}$

其中$1_n^Tv=0$，故也有$r^Tv=0$。令$\bar v=-\alpha\nabla f(\bar x)$。

定义坐标变换

$\begin{aligned} u&=v-\bar v，\,&y &=x-\bar x，\\ u&=Pw，\,&y&=Pz。 \end{aligned}$

由于拉普拉斯矩阵的性质，$P^TLP=\operatorname{diag}( 0,R^TLR)$。同时，$r^TPw=r^T(v-\bar v)=r^T\bar v$，$R^TPw=w_{2:n}$。

定义$h=\nabla f(y+\bar x)-\nabla f(\bar x)$，有

$\begin{aligned} \dot w_1&=0，\\ \dot w_{2:n}&=\alpha\beta R^TLRz_{2:n}，\\ \dot z_1&=-\alpha r^Th，\\ \dot z_{2:n}&=-\alpha R^Th-\beta R^TLRz_{2:n}-w_{2:n}。 \end{aligned}$

Section 5.2中的应用

令$\tilde z_{2:n}(t)=z_{2:n}(t_k)-z_{2:n}(t)=R^TP(z(t_k)-z(t))=R^T(x(t_k)-x(t))$，则有

$\tilde z_{2:n}^T(t)\tilde z_{2:n}(t)=(x(t_k)-x(t))^TRR^T(x(t_k)-x(t))=(x(t_k)-x(t))^T\Pi(x(t_k)-x(t))。$

由于$\Pi$是幂等的，即$\Pi=\Pi^2$。因此，$\|\tilde z_{2:n}(t)\|=\|\Pi(x(t_k)-x(t))\|$。

令$p=[z^T,w_{2:n}^T]^T$，同样的由于$\Pi$的幂等性，有

$p^Tp=z^Tz+w_{2:n}^Tw_{2:n}=y^TPP^Ty+wP^TRR^T Pw=(x-\bar x)^T(x-\bar x)+(v-\bar v)^T\Pi(v-\bar v)$

因此，$\|p\|=\sqrt{\|x-\bar x\|^2+\|\Pi(v-\bar v)\|^2}$。

题外话

此外，简单记录下第一节所看论文的另外一些收获。

两个定理

证明收敛性和有界性用到的两个定理^[3]。

Lemma 3.4. (Comparison lemma) Consider the scalar differential equation

$\dot u=f(t,u),\,u(t_0)=u_0$

where $f(t,u)$ is continuous in $t$ and locally Lipschitz in $u$, for all $t\geq 0$ and all $u\in J\subset \mathbb R$. Let $[t_0,T)$ ($T$ could be infinity) be the maximal interval of existence of the solution $u(t)$ and suppose $u(t)\in J$ for all $t\in[t_0,T)$. Let $v(t)$ be a continuous function whose upper right-hand derivative $D^+v(t)$ satisfies the differential inequality

$D^+v(t)\leq f(t,v(t)),\,v(t_0)\leq u_0,$

with $v(t)\in J$ for all $t\in[t_0,T)$. Then, $v(t)\leq u(t)$ for all $t\in[t_0,T)$.

可以知道，当$\dot v(t)\leq \dot u(t)$且$v(t_0)\leq u(t_0)$时，$v(t)\leq u(t)$。

Theorem 4.10. Let $x=0$ be an equilibrium point for $\dot x=f(t,x)$ and $D\subset \mathbb R^n$ be a domain containing $x=0$. Let $V:[0,\infty)\times D\to \mathbb R$ be a continuously differentiable function such that

$\begin{aligned} k_1\|x\|^\alpha\leq V(t,x)&\leq k_2\|x\|^\alpha,\\ \frac{\partial V}{\partial t}+\frac{\partial V}{\partial x}f(t,x)&\leq -k_3\|x\|^\alpha, \end{aligned}$

$\forall t\geq 0$ and $\forall x\in D$, where $k_1$, $k_2$, $k_3$, and $a$ are positive constants. Then, $x=0$ is exponentially stable. If the assumptions hold globally, then $x=0$ is globally exponentially stable.

可以知道，当上述定理中的条件满足时，我们有$\dot V\leq -\frac{k_3}{k_2}V$，即不光指数收敛，且收敛速度不小于$\frac{k_3}{k_2}$。

由Lemma 3.4可知，

$V(t,x(t))\leq V(t_0,x(t_0))e^{-(k_3/k_2)(t-t_0)}。$

因此，

$\begin{aligned} \|x(t)\|&\leq \left[\frac{V(t,x(t))}{k_1}\right]^{1/\alpha}\leq\left[\frac{V(t_0,x(t_0))e^{-(k_3/k_2)(t-t_0)}}{k_1}\right]^{1/\alpha}\\ &\leq \left[\frac{k_2\|x(t_0)\|^\alpha e^{-(k_3/k_2)(t-t_0)}}{k_1}\right]^{1/\alpha}=\left(\frac{k_2}{k_1}\right)^{1/\alpha}\|x(t_0)\|e^{-(k_3/k_2a)(t-t_0)}。 \end{aligned}$

微分方程求解

使用Lemma 3.4证明收敛性，本质是把一个复杂的微分方程求解问题，转化成一个相对容易的微分方程来求解。

以第一节所看论文中证明有界性时的一个问题为例。已知

$\dot x\leq a(1+x)+b(1+x)^2,\,x(0)=0$

现在要证明$x$在时间$\tau$内有界$\zeta$，并求出$\tau$的值。

应用Lemma 3.4，若存在$\dot y=a(1+y)+b(1+y)^2$，$y(0)=0$，那么$x\leq y$，$\forall t\geq 0$。

分离变量，求解微分方程，参考步骤^[4]如下

$\begin{aligned} t+C=\int dt &=\int \frac{dy}{a(1+y)+b(1+y)^2}\\ &=\int \frac{dy}{b\left(1+y+\frac{a}{2b}\right)^2-\frac{a^2}{4b}}\\ &=\frac{1}{b}\int \frac{dz}{z^2-\frac{a^2}{4b^2}} ,\quad \left(z=1+y+\frac{a}{2b}\right)\\ &=\frac{1}{a}\int \left(\frac{dz}{z-\frac{a}{2b}}-\frac{dz}{z+\frac{a}{2b}}\right)\\ &=\frac{1}{a}\ln \left|z-\frac{a}{2b}\right|-\frac{1}{a}\ln \left|z+\frac{a}{2b}\right|\\ &=\frac{1}{a}\ln \left|1+y\right|-\frac{1}{a}\ln \left|1+y+\frac{a}{b}\right| \end{aligned}$

假设$y,a,b\geq 0$。令$y=t=0$，可得$aC=\ln (\frac{b}{a+b})$，则有

$e^{at+aC}=\frac{b}{a+b}e^{at}=\frac{by+b}{by+a+b}$

变换为$y$关于$t$的函数

$y(t,0)=\frac{(a+b)(e^{at}-1)}{-be^{at}+a+b}$

再令$y(\tau,0)=\zeta$，得到

$\tau=\frac{1}{a}\ln\left(1+\frac{a\zeta}{a+b(1+\zeta)}\right)$