飞桨强化学习从零实践(一):基于价值的方法
写在前面
不要重复造轮子,学会使用轮子。
本文源于百度AI平台飞桨学院《世界冠军带你从零实践强化学习》课程中我自己的心得和理解,感谢科科老师这几天精彩的讲解,带我们从小乌龟(Sarsa、Q-learning),到倒立摆(DQN,PG),再到四旋翼飞行器(DDPG),逐步领略强化学习的魅力。本文旨在介绍PARL框架的使用方法,并从模型的理解和代码的构建角度来整理所学内容,不求详尽但求简洁明了,看完都能学会Model、Algorithm、Agent的构建方法。我认为强化学习中对算法每一个概念的理解很重要,你可以不懂公式的推导,但是只要你理解了算法框图中的每一个步骤,那你就能够灵活的应用PARL框架去解决自己的问题。为了让大家理解代码的模块化构建,这篇文章只介绍Sarsa、Q-learning和DQN,前两者只用了一个Agent函数,后者用了PARL的Model、Algorithm、Agent模块,对比两种构建方式的不同,我们就可以很轻松的举一反三,PG和DDPG同样也可以用这三大模块构建。
依赖库是python初学者永远的痛点,相信很多人都有网上查到代码,本地一运行各种报错的经历,本文在各代码之前列举了所需依赖库,希望大家自己研究代码时能一次跑通。所有课程官方代码和作业答案都已上传至我的GitHub,欢迎大家star一下,文章中有问题或疏漏的地方大家也可以直接查看源码。
开始之前我希望大家都具有python编程基础,一定程度上掌握Numpy的用法,这个库真的是很有用。没用过的可以参考我之前的文章(查看这里)。学习过程中也可以参考大神的文章,推荐Tiny Tony、Mr.郑先生_、hhhsy、叶强。
强化学习——从尝试到决策
每个人都是过去经验的总和。
初识强化学习
强化学习(Reinforcement learning,简称RL)是机器学习中的一个领域,强调如何基于环境而行动,以取得最大化的预期利益。核心思想是:智能体(agent)在环境(environment)中学习,根据环境的状态(state)或观测(observation),执行动作(action),并根据环境的反馈 (reward)来指导更好的动作。

作为机器学习三巨头之一,强化学习和监督学习以及非监督学习关系如下图。
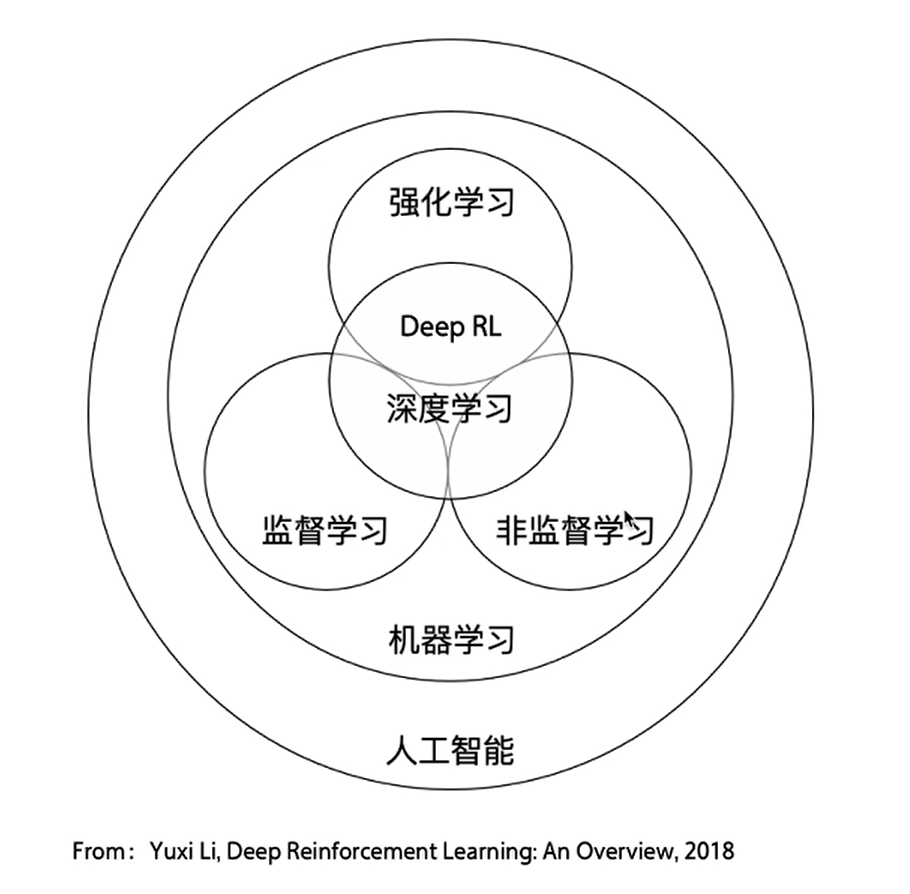
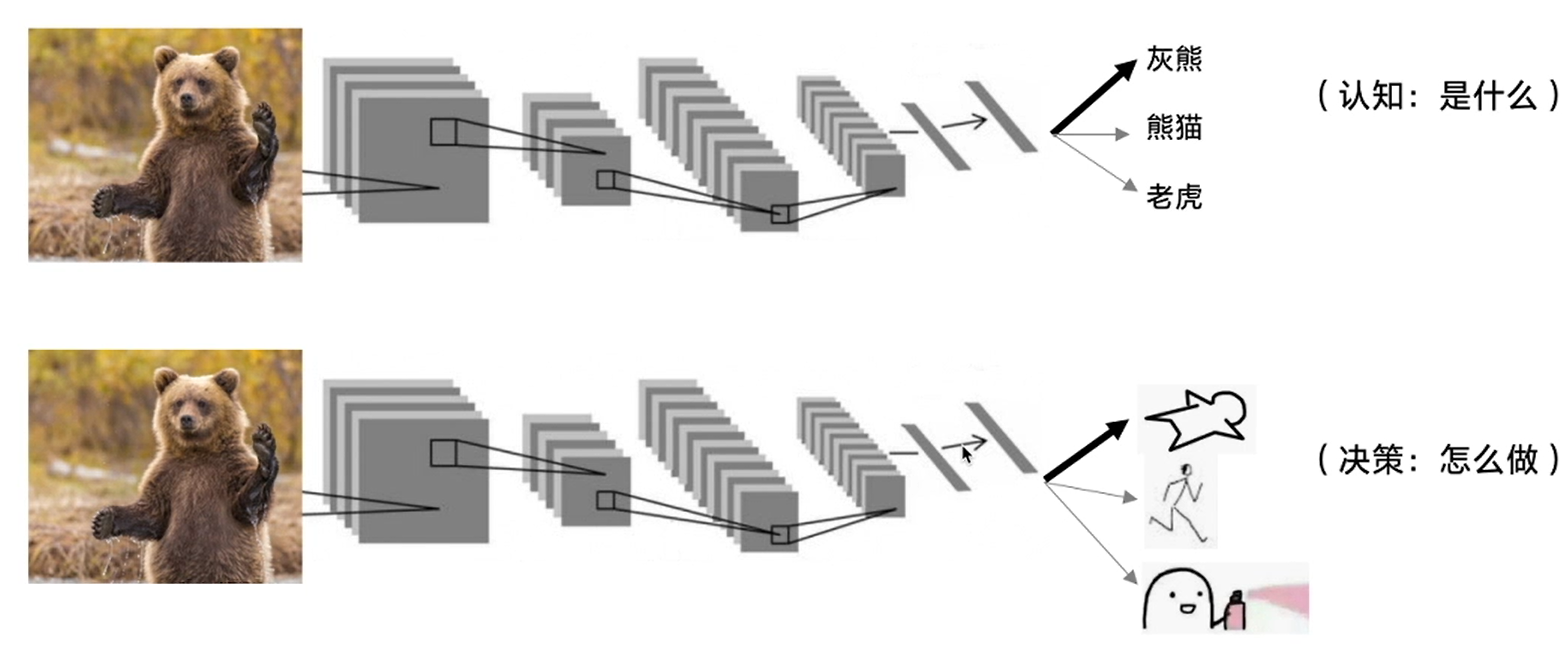
监督学习关注的是认知,而强化学习关注的是决策。简单的说,前者学习经验,后者运用经验。同样都是一张小熊的图片,监督学习输出的是灰熊、熊猫还是老虎,强化学习输出的是装死、逃跑还是干一架。
强化学习的分类和方法
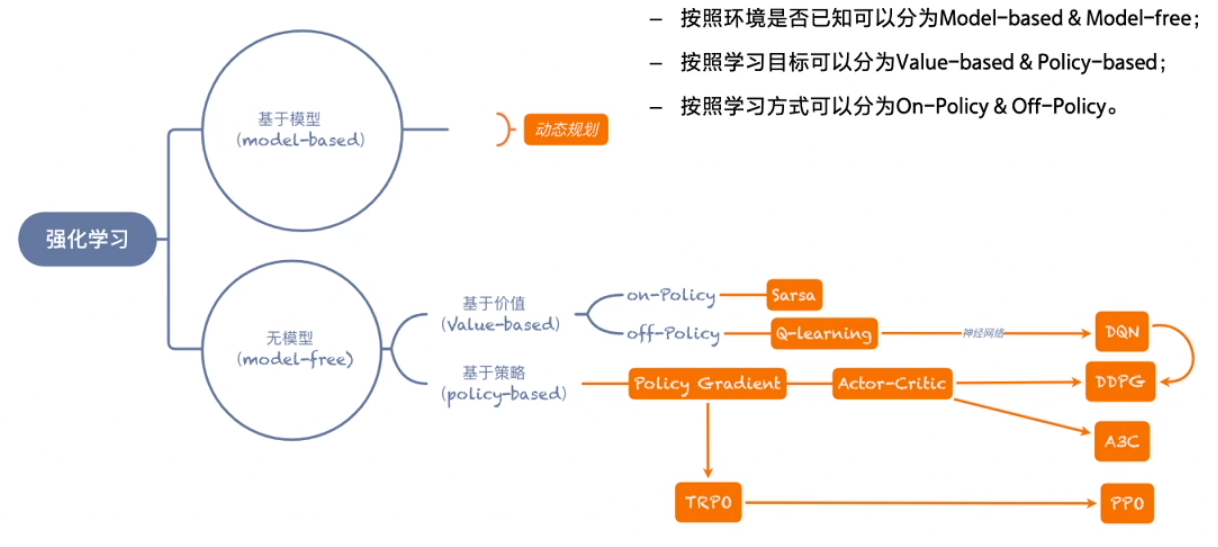
强化学习主要关注的是无模型的问题,在未知的环境中进行探索学习,在生活中有广泛的应用。
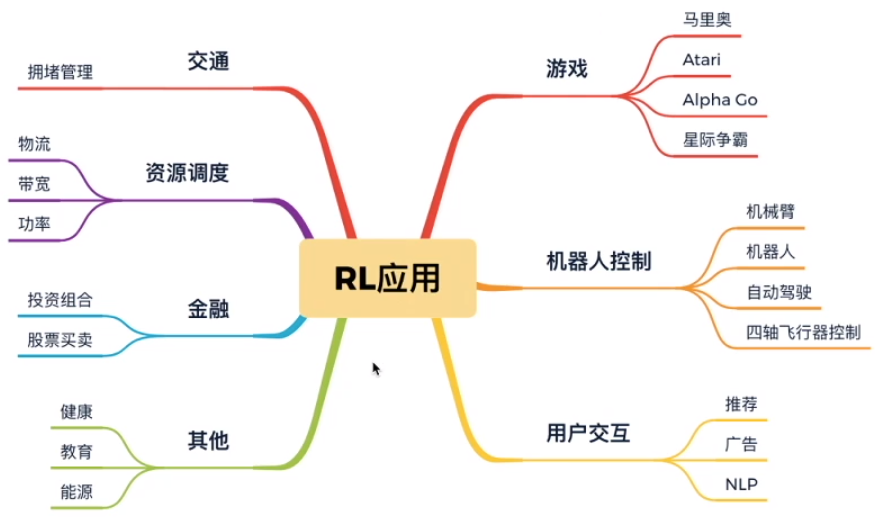
其探索方案有二:
- 基于价值的方法(Q函数)
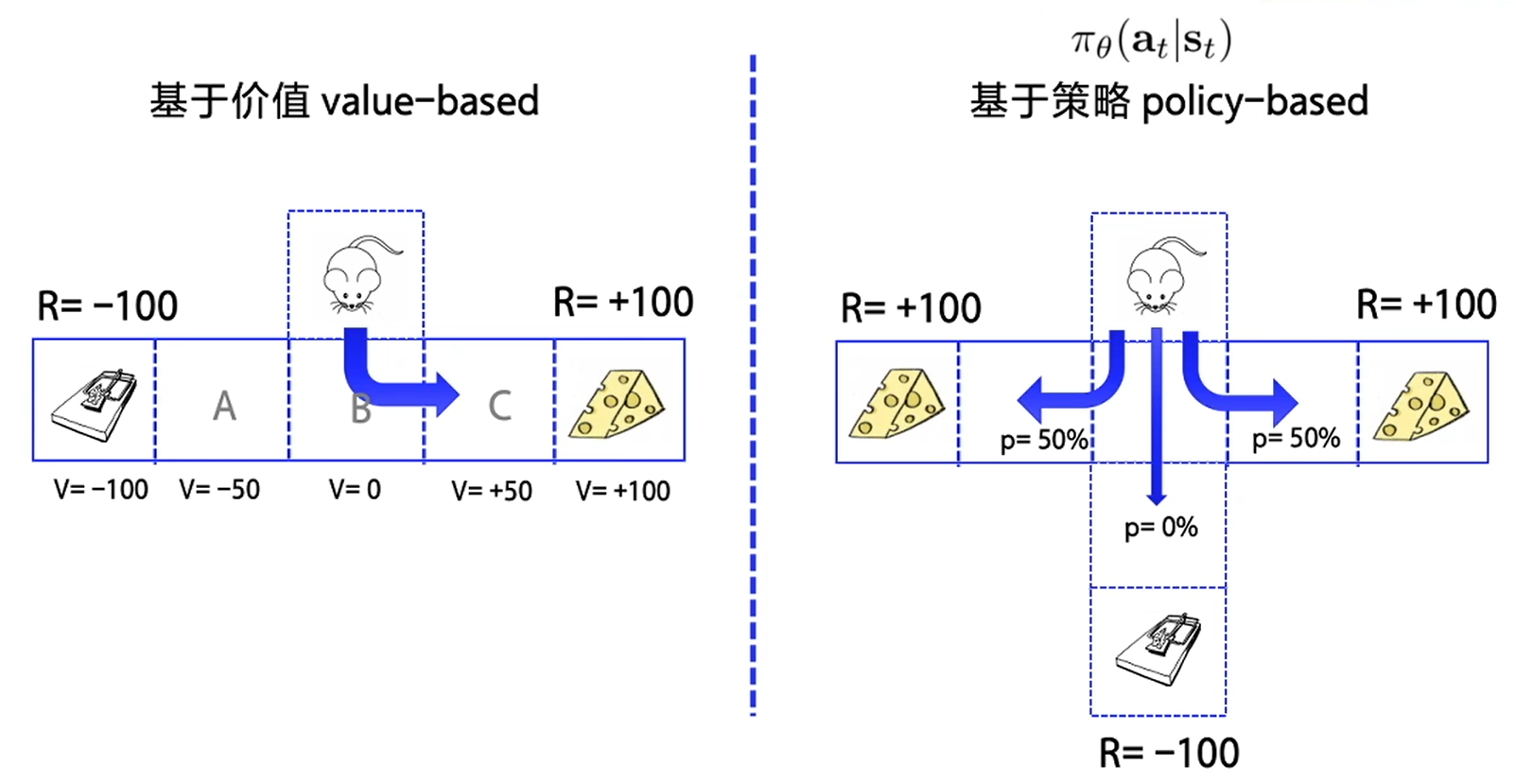
给每个状态都赋予一个价值的概念,来代表这个状态是好还是坏,这是一个相对的概念,让智能体往价值最高的方向行进。基于价值是确定性的。 - 基于策略的方法(Policy)
制定出多个策略,策略里的每个动作都有一定的概率,并让每一条策略走到底,最后查看哪个策略是最优的。基于策略是随机性的。
PARL框架和GYM环境
- 强化学习经典环境库GYM将环境(Env)交互接口规范化为:重置环境
reset()、交互step()、渲染render()。 - 强化学习框架库PARL将强化学习框架抽象为:
Model、Algorithm、Agent三层,使得强化学习算法的实现和调试更方便和灵活。(前两者有神经网络才用得上)
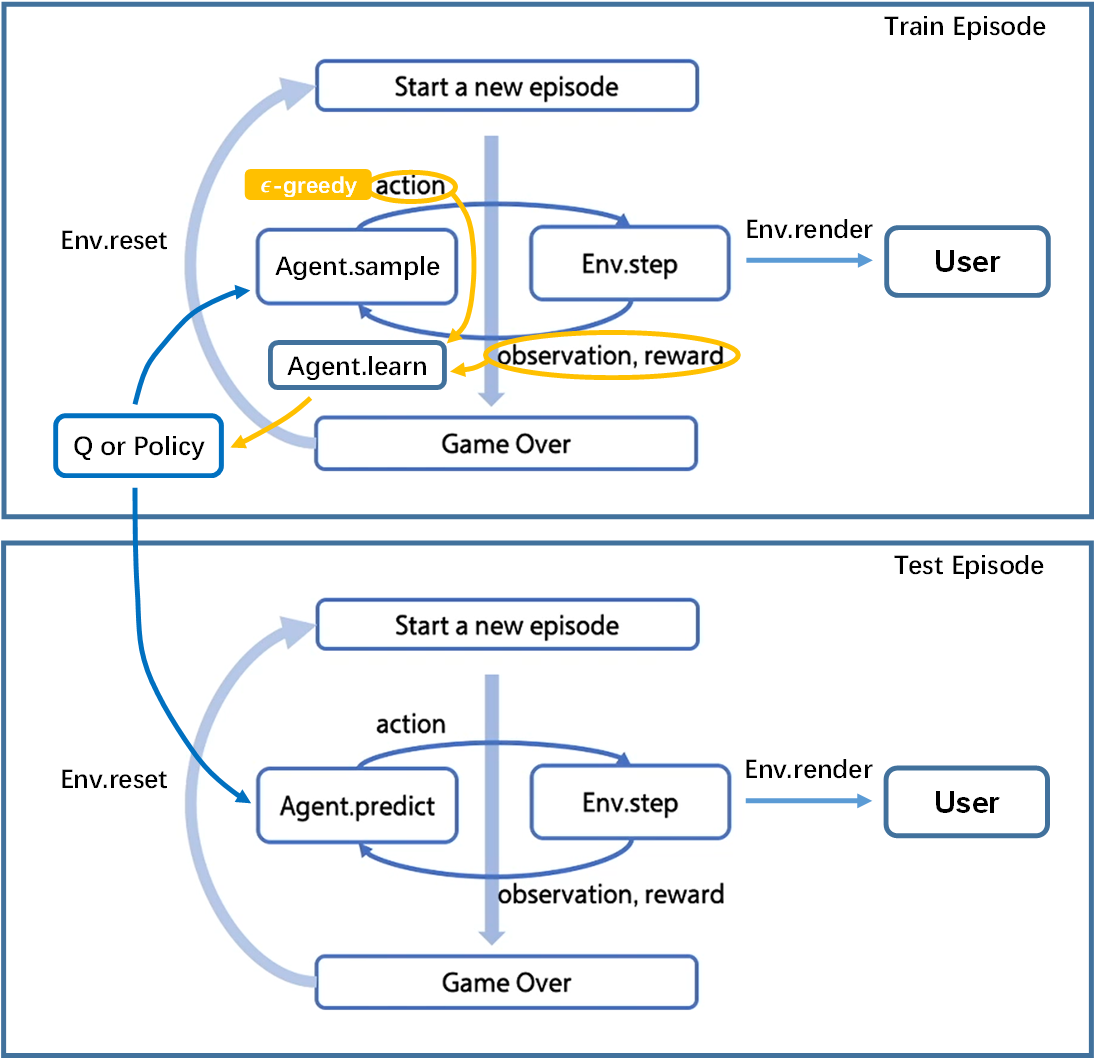
Agent的训练(Train)和测试(Test)过程直接上图展示如下。
本文所需全部依赖库代码如下,paddlepaddle默认使用CPU版本,可自行选用GPU版本,这里不再赘述。
# 可以直接 pip install -r requirements.txt
pip install paddlepaddle==1.6.3
pip install parl==1.3.1
pip install gym
pip install atari-py
pip install rlschool==0.3.1
基于表格型方法求解RL
没有什么比前人走过的路(Q)更有价值(V)。
序列决策的经典表达(MDP)
某一状态信息包含了所有相关的历史,只要当前状态可知,所有的历史信息都不再需要,当前状态就可以决定未来,则认为该状态具有马尔科夫性。马尔可夫决策过程(MDP)是序列决策的数学模型,它是一个无记忆的随机过程,可以用一个元组<S,P>表示,其中S是有限数量的状态集,P是状态转移概率矩阵。
强化学习中我们引入奖励R和动作A来描述环境,构成MDP五元组<S,A,P,R,>,其中P函数表示环境的随机性,R函数其实是P函数的一部分,表示获得的收益,是衰减因子以适当的减少对未来收益的考虑。
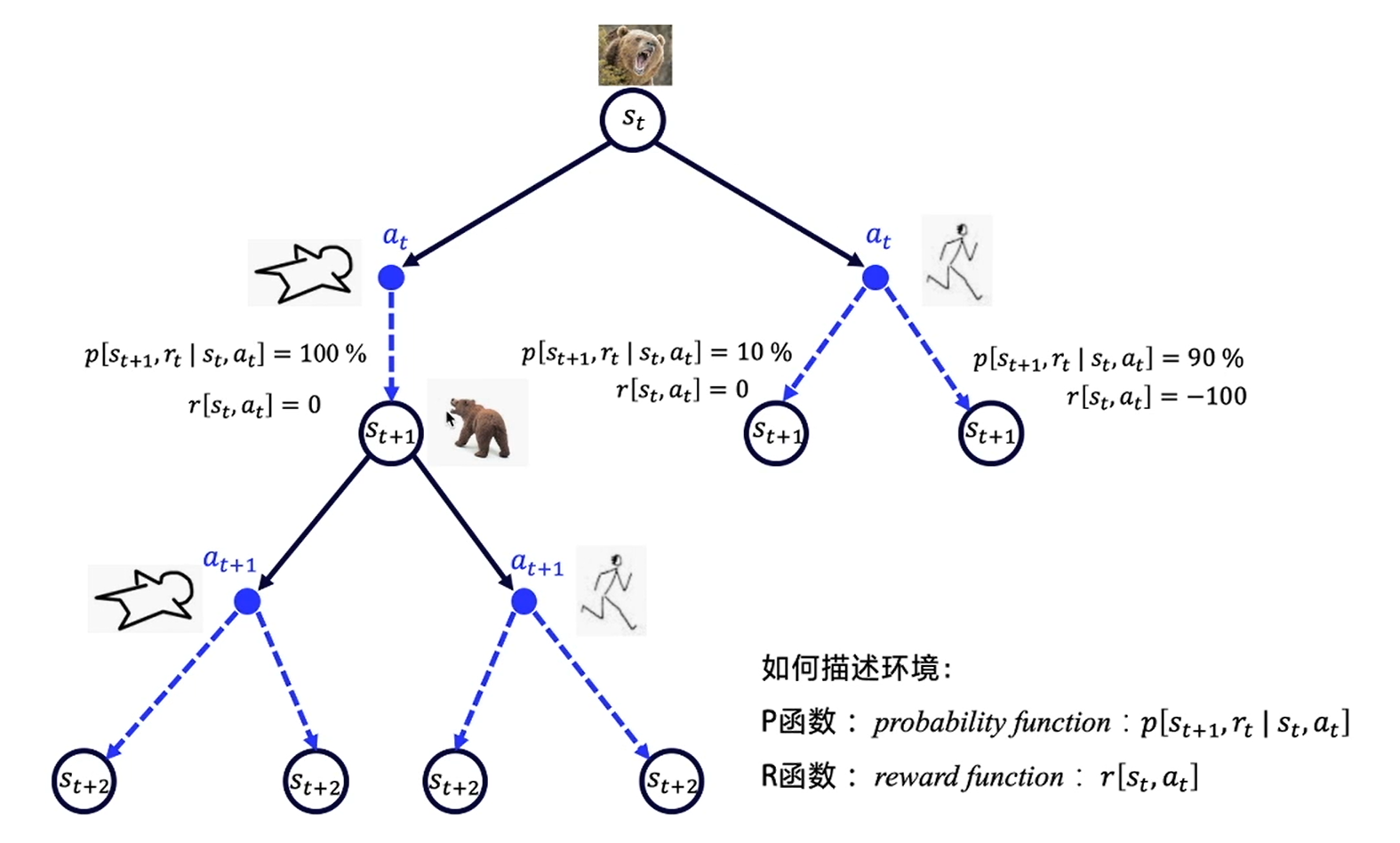
同样以熊问题为例,对应的是Model-free的情况,即P函数和R函数都未知的情况。这时我们用价值V代表某一状态的好坏,用Q函数来代表某个状态下哪个动作更好,即状态动作价值。
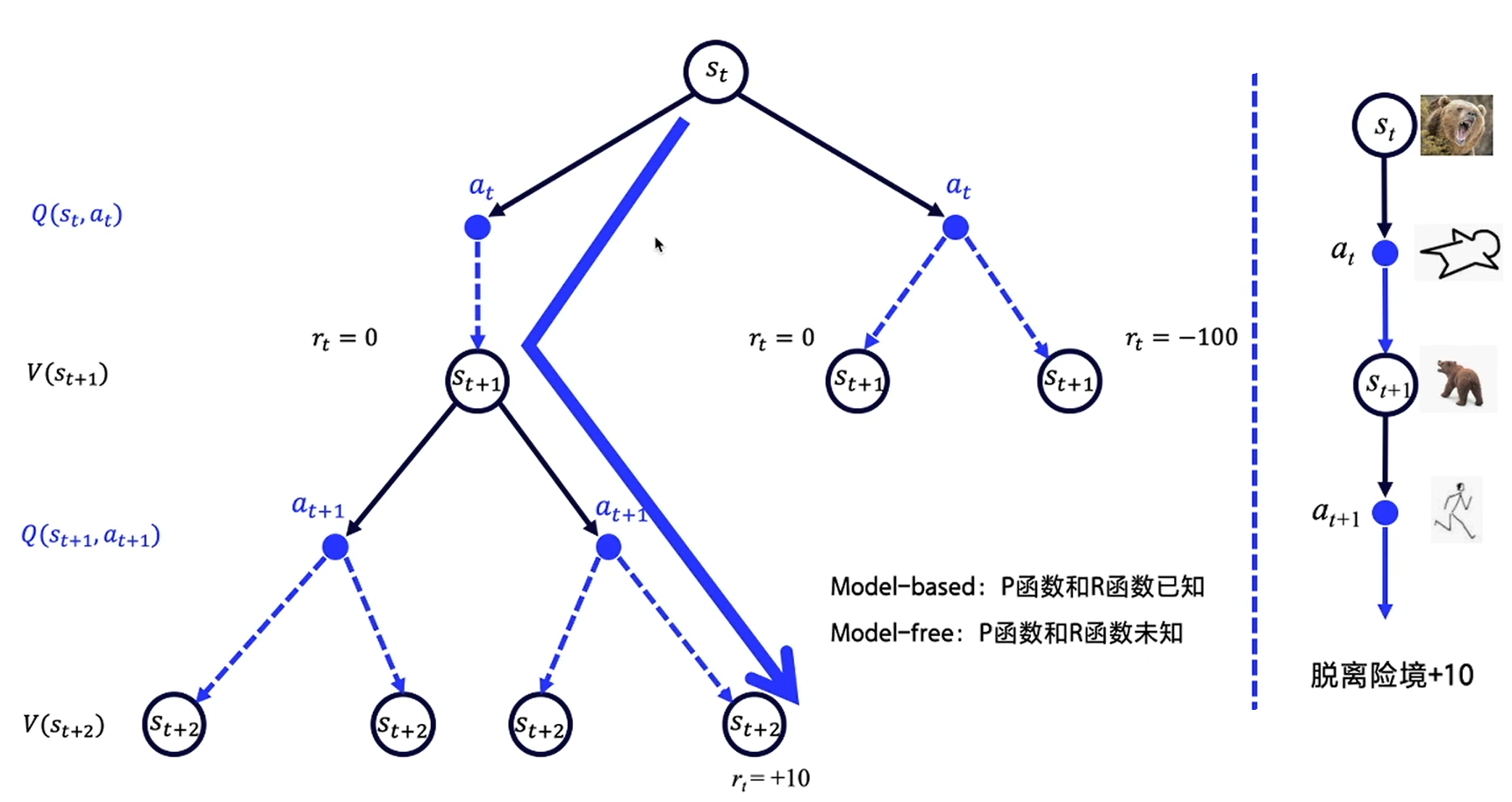
现实世界中,奖励R往往是延迟的,所以一般会从当前时间点开始,对后续可能得到的收益累加,以此来计算当前的价值。但是有时候目光不要放得太长远,对远一些的东西当作近视看不见就好。适当地引入一个衰减因子,再去计算未来的总收益,的值在0-1之间,时间点越久远,对当前的影响也就越小。
状态动作价值(Q)的求解
假设人走在树林里,先看到树上有熊爪后看到熊,接着就看到熊发怒了,经过很多次之后,原来要见到熊才瑟瑟发抖的,后来只要见到树上有熊爪就会有晕眩和害怕的感觉。也就是说,在不断地训练之后,下一个状态的价值可以不断地强化、影响上一个状态的价值。
这样的迭代状态价值的强化方式被称为时序差分(Temporal Difference)。单步求解Q函数,用来近似,以迭代的方式简化数学公式,最终使得逼近目标值。这里的目标值就是前面提到的未来收益之和。注意实际上是由当前计算出来的,因此。
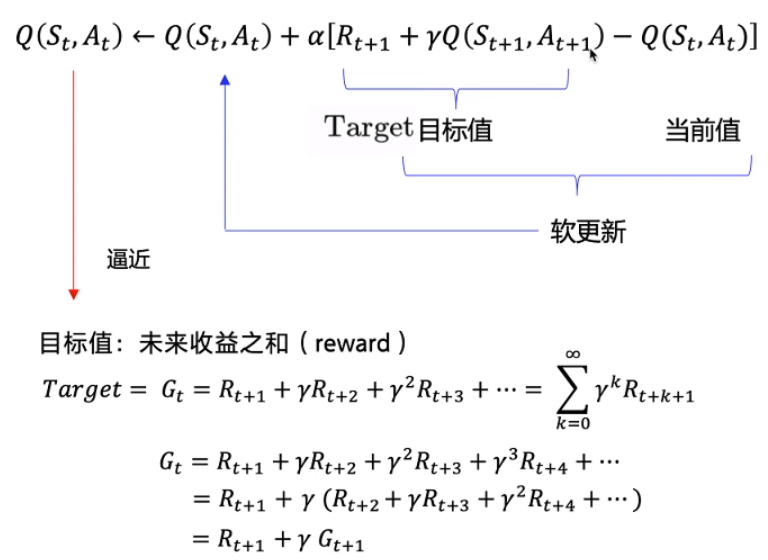
Sarsa和Q-learning
Sarsa全称是state-action-reward-state’-action’,目的是学习特定的state下,特定action的价值Q,最终建立和优化一个Q表格,以state为行,action为列,根据与环境交互得到的reward来更新Q表格,更新公式即为上面的迭代公式。Sarsa在训练中为了更好的探索环境,采用ε-greedy方式(如下图)来训练,有一定概率随机选择动作输出。

Q-learning也是采用Q表格的方式存储Q值,探索部分与Sarsa是一样的,采用ε-greedy方式增加探索。
- Q-learning跟Sarsa不一样的地方是更新Q表格的方式,即learn()函数。
- Sarsa是on-policy,先做出动作再learn,Q-learning是off-policy,learn时无需获取下一步动作。
二者更新Q表格的方式分别为:
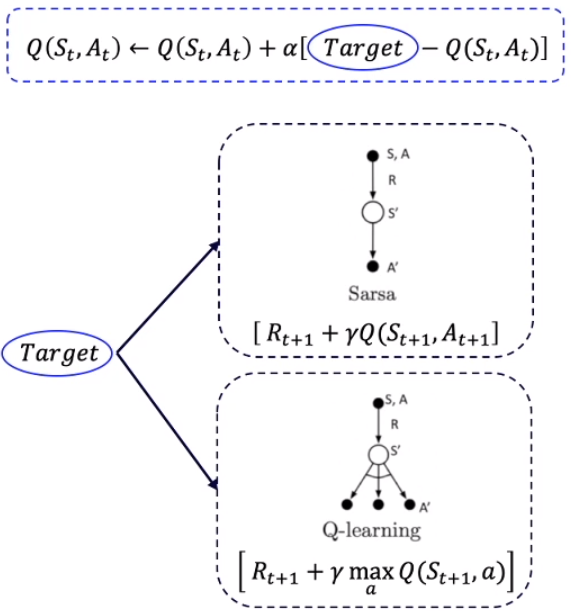
二者算法对比如下图所示,有三处不同点。

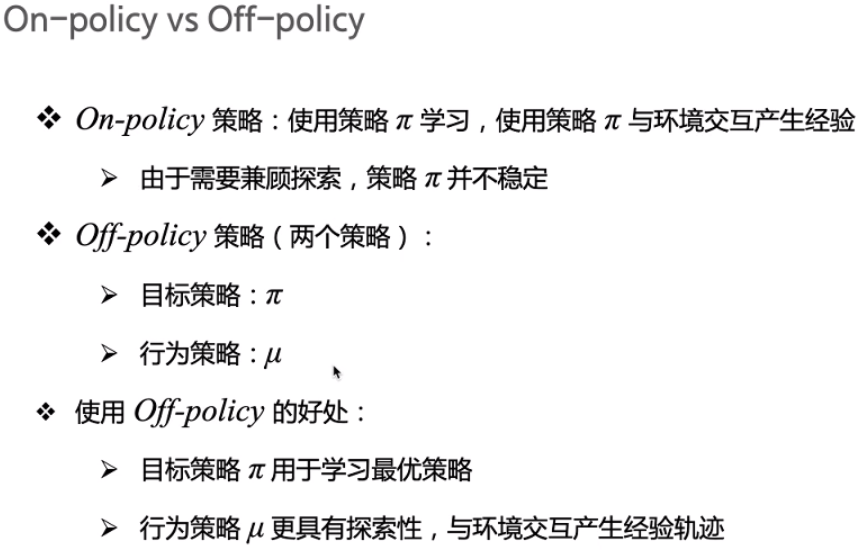
on-policy优化的是目标策略,用下一步一定会执行的动作来优化Q表格;off-policy实际上有两种不同的策略,期望得到的目标策略和大胆探索的行为策略,在目标策略的基础上用行为策略获得更多的经验。
代码构建与演示
import numpy as np
Sarsa Agent构建
class SarsaAgent(object):
def __init__(self,
obs_n,
act_n,
learning_rate=0.01,
gamma=0.9,
e_greed=0.1):
self.act_n = act_n # 动作维度,有几个动作可选
self.lr = learning_rate # 学习率
self.gamma = gamma # reward的衰减率
self.epsilon = e_greed # 按一定概率随机选动作
self.Q = np.zeros((obs_n, act_n)) # 构建Q表格
# 根据输入观察值,采样输出的动作值,带探索
def sample(self, obs):
if np.random.uniform(0, 1) < (1.0 - self.epsilon): #根据table的Q值选动作
action = self.predict(obs)
else:
action = np.random.choice(self.act_n) #有一定概率随机探索选取一个动作
return action
# 根据输入观察值,预测输出的动作值
def predict(self, obs):
Q_list = self.Q[obs, :]
maxQ = np.max(Q_list)
action_list = np.where(Q_list == maxQ)[0] # maxQ可能对应多个action(where返回一个tuple,需要取[0])
action = np.random.choice(action_list) # 随机选择一个action
return action
# 学习方法,也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, next_action, done):
""" on-policy
obs: 交互前的obs, s_t
action: 本次交互选择的action, a_t
reward: 本次动作获得的奖励r
next_obs: 本次交互后的obs, s_t+1
next_action: 根据当前Q表格, 针对next_obs会选择的动作, a_t+1
done: episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 没有下一个状态了
else:
target_Q = reward + self.gamma * self.Q[next_obs,
next_action] # Sarsa
self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q
Q-learning Agent构建
class QLearningAgent(object):
def __init__(self,
obs_n,
act_n,
learning_rate=0.01,
gamma=0.9,
e_greed=0.1):
self.act_n = act_n # 动作维度,有几个动作可选
self.lr = learning_rate # 学习率
self.gamma = gamma # reward的衰减率
self.epsilon = e_greed # 按一定概率随机选动作
self.Q = np.zeros((obs_n, act_n))
# 根据输入观察值,采样输出的动作值,带探索
def sample(self, obs):
# 内容略,和sarsa一样
return action
# 根据输入观察值,预测输出的动作值
def predict(self, obs):
# 内容略,和sarsa一样
return action
# 学习方法,也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, done):
""" off-policy
obs: 交互前的obs, s_t
action: 本次交互选择的action, a_t
reward: 本次动作获得的奖励r
next_obs: 本次交互后的obs, s_t+1
done: episode是否结束
"""
predict_Q = self.Q[obs, action]
if done:
target_Q = reward # 没有下一个状态了
else:
target_Q = reward + self.gamma * np.max(
self.Q[next_obs, :]) # Q-learning
self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q
训练过程代码如下:
# train.py
import gym
from gridworld import CliffWalkingWapper, FrozenLakeWapper
from agent import SarsaAgent
import time
def run_episode(env, agent, render=False):
total_steps = 0 # 记录每个episode走了多少step
total_reward = 0
obs = env.reset() # 重置环境, 重新开一局(即开始新的一个episode)
action = agent.sample(obs) # 根据算法选择一个动作
while True:
next_obs, reward, done, _ = env.step(action) # 与环境进行一个交互
next_action = agent.sample(next_obs) # 根据算法选择一个动作
# 训练 Sarsa 算法
agent.learn(obs, action, reward, next_obs, next_action, done)
action = next_action # 存储上一个动作
# 训练 q-learing 算法
# agent.learn(obs, action, reward, next_obs, done)
obs = next_obs # 存储上一个观察值
total_reward += reward
total_steps += 1 # 计算step数
if render:
env.render() #渲染新的一帧图形
if done:
break
return total_reward, total_steps
def test_episode(env, agent):
total_reward = 0
obs = env.reset()
while True:
action = agent.predict(obs) # greedy
next_obs, reward, done, _ = env.step(action)
total_reward += reward
obs = next_obs
time.sleep(0.5)
env.render()
if done:
print('test reward = %.1f' % (total_reward))
break
def main():
# env = gym.make("FrozenLake-v0", is_slippery=False) # 0 left, 1 down, 2 right, 3 up
# env = FrozenLakeWapper(env)
env = gym.make("CliffWalking-v0") # 0 up, 1 right, 2 down, 3 left
env = CliffWalkingWapper(env)
agent = SarsaAgent(
obs_n=env.observation_space.n,
act_n=env.action_space.n,
learning_rate=0.1,
gamma=0.9,
e_greed=0.1) # 或 QLearningAgent
is_render = False
for episode in range(500):
ep_reward, ep_steps = run_episode(env, agent, is_render)
print('Episode %s: steps = %s , reward = %.1f' % (episode, ep_steps,
ep_reward))
# 每隔20个episode渲染一下看看效果
if episode % 20 == 0:
is_render = True
else:
is_render = False
# 训练结束,查看算法效果
test_episode(env, agent)
if __name__ == "__main__":
main()
可以看到二者区别全在learn函数,训练过程的差别也仅在learn的输入是否有next_action。大家可以尝试用命令行运行以下演示代码(这里下载),训练环境是悬崖问题(CliffWalking)。作业中的冰湖问题(FrozenLake)见.\tutorials\homework文件夹。
# sarsa 演示
cd .\tutorials\lesson2\sarsa
python .\train.py
# q-learing 演示
cd .\tutorials\lesson2\q_learning
python .\train.py
最终结果如下面的GIF所示。可以看出来Sarsa比较保守,会选择下限最高的路线,即尽可能远离悬崖的路线,虽然路程远了,但至少掉下悬崖的风险就小了很多;而Q-learning比较激进,会选择上限最高的路线,即路程最近的路线,但存在些微扰动便可能掉下悬崖。
Sarsa训练图:

Q-learning训练图:

基于神经网络方法求解RL
选择(A)有限,而人生(S)无限。
神经网络近似Q函数
前面提到的悬崖问题,状态(S)总量很少,但实际生活中,很多常见问题的状态都是数量庞大的,如象棋、围棋等。即使用Q表格装下所有状态,表格可能占用极大内存,表格的查找也相当费时。我们就可以用带参数的Q函数来近似Q表格,比如可以用多项式函数或者神经网络,优势是只需要输出少量参数,同时能实现状态泛化。
神经网络结构如下图所示。
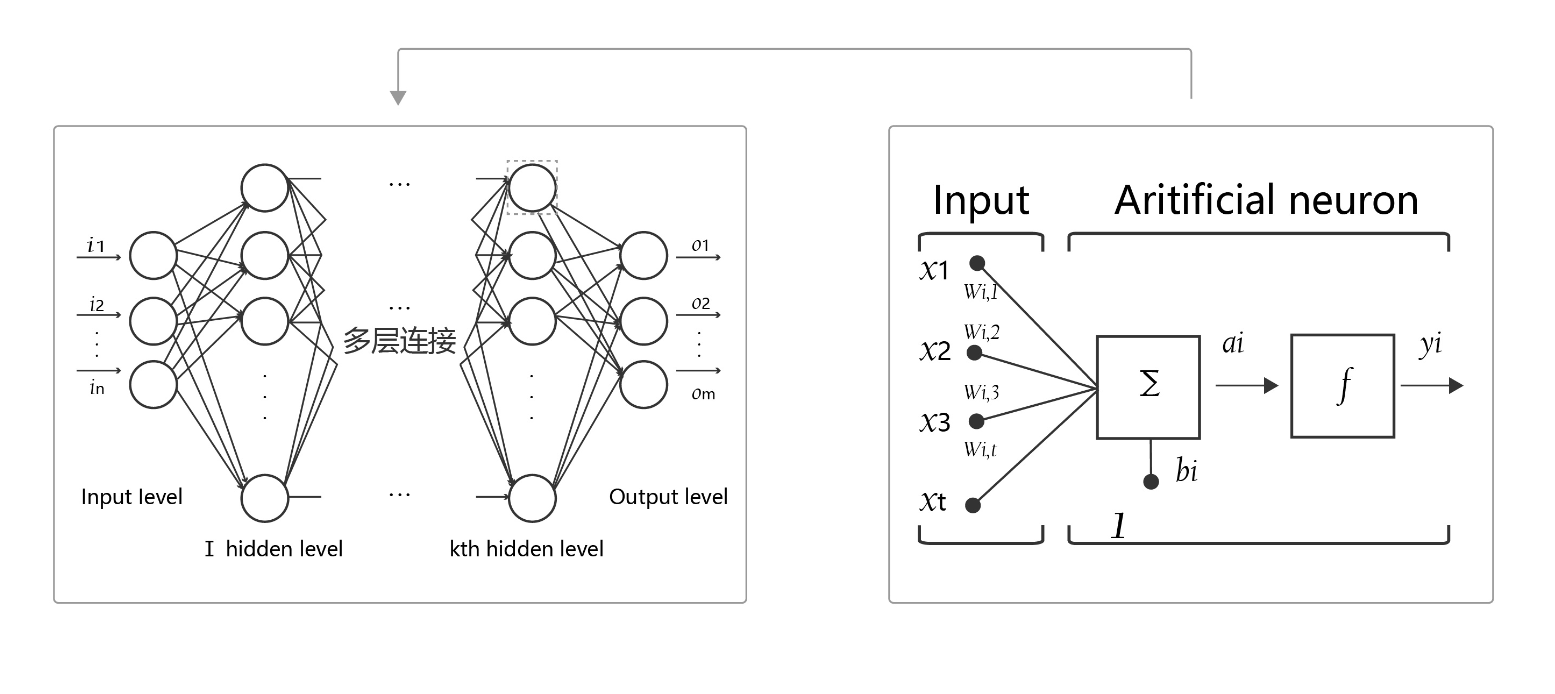
- 神经元:神经网络中每个节点称为神经元,由两部分组成:
- 加权和:将所有输入加权求和。
- 非线性变换(激活函数):加权和的结果经过一个非线性函数变换,让神经元计算具备非线性的能力。
- 多层连接: 大量这样的节点按照不同的层次排布,形成多层的结构连接起来,即称为神经网络。
- 前向计算: 从输入计算输出的过程,顺序从网络前至后。
- 计算图: 以图形化的方式展现神经网络的计算逻辑又称为计算图。我们也可以将神经网络的计算图以公式的方式表达为
由此可见,神经网络的本质是一个含有很多参数的“大公式”。
DQN:入门deep RL
DQN本质上是一个Q-learning算法,但使用神经网络来近似替代Q表格。
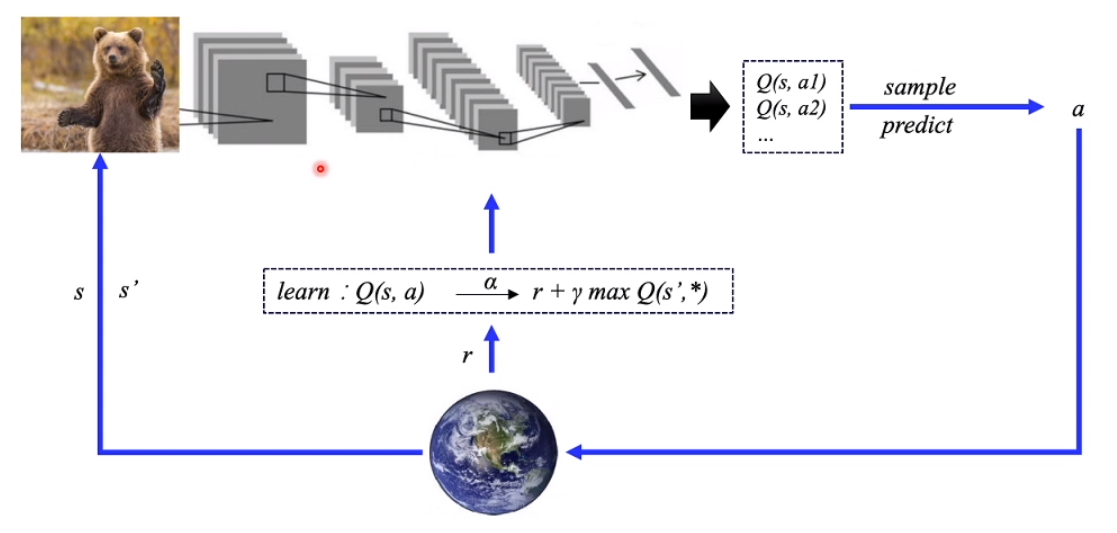
类比监督学习的训练,DQN的训练过程也非常地类似,它输入的是一批状态(S),输出的是对应的Q。计算输出的Q与Target Q的均方差,进行优化,以此更新神经网络参数。
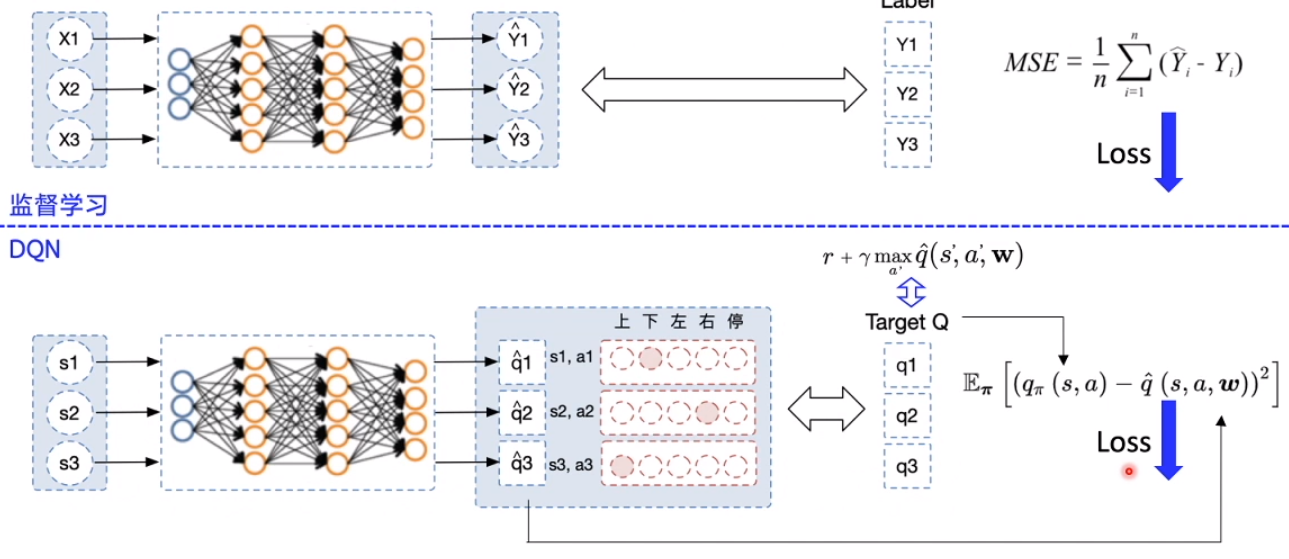
在Q-learning的基础上,DQN提出了两个技巧使得Q网络的更新迭代更稳定:
- 经验回放 (Experience Replay):主要解决样本关联性和利用效率的问题。使用一个经验池(buffer)存储多条经验(s,a,r,s’),再从中随机抽取一批(batch)数据送去训练。
- 固定Q目标 (Fixed-Q-Target):主要解决算法训练不稳定的问题。每隔一段时间复制一次网络参数(w),保证用于计算Target Q的Q函数不变。
代码构建与演示
这部分代码构建展示了PARL框架的基本用法,即Model、Algorithm、Agent嵌套。Algorithm是Agent的一部分,Model又是Algorithm的一部分,相比较前文中只有一个Agent的简单代码模块性更好,但理解起来也更复杂,容我慢慢道来。
import parl
from parl import layers
import paddle.fluid as fluid
import copy
import numpy as np
Model用来定义前向(Forward)网络,用户可以自由的定制自己的神经网络结构。
class Model(parl.Model):
def __init__(self, act_dim):
hid1_size = 128
hid2_size = 128
# 3层全连接(fc)网络,act选择激活函数,不使用激活函数即线性
self.fc1 = layers.fc(size=hid1_size, act='relu')
self.fc2 = layers.fc(size=hid2_size, act='relu')
self.fc3 = layers.fc(size=act_dim, act=None)
def value(self, obs):
# 前向计算 Q实际上是一个二维数组
# 输入state,输出所有action对应的Q,[Q(s,a1), Q(s,a2), Q(s,a3)...]
h1 = self.fc1(obs)
h2 = self.fc2(h1)
Q = self.fc3(h2)
return Q
Algorithm定义了具体的算法来更新前向网络(Model),也就是通过定义损失函数来更新Model,和算法相关的计算都放在algorithm中。
# from parl.algorithms import DQN # 也可以直接从parl库中导入DQN算法
class DQN(parl.Algorithm):
def __init__(self, model, act_dim=None, gamma=None, lr=None):
""" DQN algorithm
Args:
model (parl.Model): 定义Q函数的前向网络结构
act_dim (int): action空间的维度,即有几个action
gamma (float): reward的衰减因子
lr (float): learning rate 学习率.
"""
self.model = model
self.target_model = copy.deepcopy(model)
# 参数的类型要求,且必须有输入
assert isinstance(act_dim, int)
assert isinstance(gamma, float)
assert isinstance(lr, float)
self.act_dim = act_dim
self.gamma = gamma
self.lr = lr
def predict(self, obs):
""" 使用self.model的value网络来获取 [Q(s,a1),Q(s,a2),...]
"""
return self.model.value(obs)
def learn(self, obs, action, reward, next_obs, terminal):
""" 使用DQN算法更新self.model的value网络
"""
# 从target_model中获取 max Q' 的值,用于计算target_Q
next_pred_value = self.target_model.value(next_obs)
# dim=0指最外边的[],dim增加向内数一个[]
# 这里value都自带两个[],所以dim=1,计算里面那个[]
best_v = layers.reduce_max(next_pred_value, dim=1)
# 阻止梯度传递保证target不变,否则paddle的优化器默认迭代一步梯度
best_v.stop_gradient = True
# 判断是否是最后一条经验
terminal = layers.cast(terminal, dtype='float32')
target = reward + (1.0 - terminal) * self.gamma * best_v
pred_value = self.model.value(obs) # 获取Q预测值
# 将action转onehot向量,比如:3 => [0,0,0,1,0]
action_onehot = layers.one_hot(action, self.act_dim)
action_onehot = layers.cast(action_onehot, dtype='float32')
# 下面一行是逐元素相乘,拿到action对应的 Q(s,a)
# 比如:pred_value = [[2.3, 5.7, 1.2, 3.9, 1.4]], action_onehot = [[0,0,0,1,0]]
# ==> pred_action_value = [[3.9]]
pred_action_value = layers.reduce_sum(
layers.elementwise_mul(action_onehot, pred_value), dim=1)
# 计算 Q(s,a) 与 target_Q的均方差,得到loss
cost = layers.square_error_cost(pred_action_value, target)
cost = layers.reduce_mean(cost)
optimizer = fluid.optimizer.Adam(learning_rate=self.lr) # 使用Adam优化器
optimizer.minimize(cost)
return cost
def sync_target(self):
""" 把 self.model 的模型参数值同步到 self.target_model
"""
# 同步参数就行,比直接copy效率高
self.model.sync_weights_to(self.target_model)
Agent负责算法与环境的交互,在交互过程中把生成的数据提供给Algorithm来更新模型(Model),数据的预处理流程也一般定义在这里。
class Agent(parl.Agent):
def __init__(self,
algorithm,
obs_dim,
act_dim,
e_greed=0.1,
e_greed_decrement=0):
assert isinstance(obs_dim, int)
assert isinstance(act_dim, int)
self.obs_dim = obs_dim
self.act_dim = act_dim
# 将Algorithm传入Agent,即self.alg
super(Agent, self).__init__(algorithm)
self.global_step = 0
self.update_target_steps = 200
# 每隔200个training steps再把model的参数复制到target_model中
self.e_greed = e_greed # 有一定概率随机选取动作,探索
self.e_greed_decrement = e_greed_decrement # 随着训练逐步收敛,探索的程度慢慢降低
def build_program(self):
# 这一部分是搭建predict和learn框架,给定数据大小和类型
# 至于输入实际数据的代码,在后面的predict和learn函数
self.pred_program = fluid.Program()
self.learn_program = fluid.Program()
with fluid.program_guard(self.pred_program):
# 搭建计算图用于 预测动作,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
self.value = self.alg.predict(obs)
with fluid.program_guard(self.learn_program):
# 搭建计算图用于 更新Q网络,定义输入输出变量
obs = layers.data(
name='obs', shape=[self.obs_dim], dtype='float32')
action = layers.data(name='act', shape=[1], dtype='int32')
reward = layers.data(name='reward', shape=[], dtype='float32')
next_obs = layers.data(
name='next_obs', shape=[self.obs_dim], dtype='float32')
terminal = layers.data(name='terminal', shape=[], dtype='bool')
self.cost = self.alg.learn(obs, action, reward, next_obs, terminal)
def sample(self, obs):
sample = np.random.rand() # 产生0~1之间的小数
if sample < self.e_greed:
act = np.random.randint(self.act_dim) # 探索:每个动作都有概率被选择
else:
act = self.predict(obs) # 选择最优动作
# 前面和sarsa基本一样,不同的是随着训练逐步收敛,探索的程度慢慢降低
self.e_greed = max(
0.01, self.e_greed - self.e_greed_decrement)
return act
def predict(self, obs): # 选择最优动作,和sample的else部分一致
# 扩展维度,因为obs是[...],但是Q是[[...]]
obs = np.expand_dims(obs, axis=0)
pred_Q = self.fluid_executor.run(
self.pred_program,
feed={'obs': obs.astype('float32')},
fetch_list=[self.value])[0]
# 降低维度,理由同上
pred_Q = np.squeeze(pred_Q, axis=0) # 若axis=0的维度len==1则移除
act = np.argmax(pred_Q) # 选择Q最大的下标,即对应的动作
return act
def learn(self, obs, act, reward, next_obs, terminal):
# 每隔200个training steps同步一次model和target_model的参数
if self.global_step % self.update_target_steps == 0:
self.alg.sync_target()
self.global_step += 1
act = np.expand_dims(act, -1)
feed = {
'obs': obs.astype('float32'),
'act': act.astype('int32'),
'reward': reward,
'next_obs': next_obs.astype('float32'),
'terminal': terminal
}
cost = self.fluid_executor.run(
self.learn_program, feed=feed, fetch_list=[self.cost])[0] # 训练一次网络
return cost
- 经验池
replay_memory:用于存储多条经验,实现经验回放。
# replay_memory.py
import random
import collections
import numpy as np
class ReplayMemory(object):
def __init__(self, max_size):
self.buffer = collections.deque(maxlen=max_size)
# 增加一条经验到经验池中
def append(self, exp):
self.buffer.append(exp)
# 从经验池中选取N条经验出来
def sample(self, batch_size):
mini_batch = random.sample(self.buffer, batch_size)
obs_batch, action_batch, reward_batch, next_obs_batch, done_batch = [], [], [], [], []
for experience in mini_batch:
s, a, r, s_p, done = experience
obs_batch.append(s)
action_batch.append(a)
reward_batch.append(r)
next_obs_batch.append(s_p)
done_batch.append(done)
return np.array(obs_batch).astype('float32'), \
np.array(action_batch).astype('float32'), np.array(reward_batch).astype('float32'),\
np.array(next_obs_batch).astype('float32'), np.array(done_batch).astype('float32')
def __len__(self):
return len(self.buffer)
训练过程代码如下:
# train.py
import os
import gym
import numpy as np
import parl
from parl.utils import logger # 日志打印工具
from model import Model
from algorithm import DQN # from parl.algorithms import DQN # parl >= 1.3.1
from agent import Agent
from replay_memory import ReplayMemory
LEARN_FREQ = 5 # 训练频率,不需要每一个step都learn,攒一些新增经验后再learn,提高效率
MEMORY_SIZE = 20000 # replay memory的大小,越大越占用内存
MEMORY_WARMUP_SIZE = 200 # replay_memory 里需要预存一些经验数据,再从里面sample一个batch的经验让agent去learn
BATCH_SIZE = 32 # 每次给agent learn的数据数量,从replay memory随机里sample一批数据出来
LEARNING_RATE = 0.001 # 学习率
GAMMA = 0.99 # reward 的衰减因子,一般取 0.9 到 0.999 不等
# 训练一个episode
def run_episode(env, agent, rpm):
total_reward = 0
obs = env.reset()
step = 0
while True:
step += 1
action = agent.sample(obs) # 采样动作,所有动作都有概率被尝试到
next_obs, reward, done, _ = env.step(action)
rpm.append((obs, action, reward, next_obs, done))
# train model 每次learn都随机抽样
if (len(rpm) > MEMORY_WARMUP_SIZE) and (step % LEARN_FREQ == 0):
(batch_obs, batch_action, batch_reward, batch_next_obs,
batch_done) = rpm.sample(BATCH_SIZE)
train_loss = agent.learn(batch_obs, batch_action, batch_reward,
batch_next_obs,
batch_done) # s,a,r,s',done
total_reward += reward
obs = next_obs
if done:
break
return total_reward
# 评估 agent, 跑 5 个episode,总reward求平均
def evaluate(env, agent, render=False):
eval_reward = []
for i in range(5):
obs = env.reset()
episode_reward = 0
while True:
action = agent.predict(obs) # 预测动作,只选最优动作
obs, reward, done, _ = env.step(action)
episode_reward += reward
if render:
env.render()
if done:
break
eval_reward.append(episode_reward)
return np.mean(eval_reward)
def main():
env = gym.make(
'CartPole-v0'
) # CartPole-v0: expected reward > 180 MountainCar-v0 : expected reward > -120
action_dim = env.action_space.n # CartPole-v0: 2
obs_shape = env.observation_space.shape # CartPole-v0: (4,)
rpm = ReplayMemory(MEMORY_SIZE) # DQN的经验回放池
# 根据parl框架构建agent
model = Model(act_dim=action_dim)
algorithm = DQN(model, act_dim=action_dim, gamma=GAMMA, lr=LEARNING_RATE)
agent = Agent(
algorithm,
obs_dim=obs_shape[0],
act_dim=action_dim,
e_greed=0.1, # 有一定概率随机选取动作,探索
e_greed_decrement=1e-6) # 随着训练逐步收敛,探索的程度慢慢降低
# 加载模型
# save_path = './dqn_model.ckpt'
# agent.restore(save_path)
# 先往经验池里存一些数据,避免最开始训练的时候样本丰富度不够
while len(rpm) < MEMORY_WARMUP_SIZE:
run_episode(env, agent, rpm)
max_episode = 2000
# start train
episode = 0
while episode < max_episode: # 训练max_episode个回合,test部分不计算入episode数量
# train part
for i in range(0, 50):
total_reward = run_episode(env, agent, rpm)
episode += 1
# test part
eval_reward = evaluate(env, agent, render=True) # render=True 查看显示效果
logger.info('episode:{} e_greed:{} Test reward:{}'.format(
episode, agent.e_greed, eval_reward))
# 训练结束,保存模型
save_path = './dqn_model.ckpt'
agent.save(save_path)
if __name__ == '__main__':
main()
大家可以尝试用命令行运行以下演示代码(这里下载),训练环境是倒立摆问题(CartPole),倒立摆可以说是强化学习中的hello world,入门必备。作业中的小车上山问题(MountainCar)见.\tutorials\homework文件夹。
# DQN 演示
cd .\tutorials\lesson3\dqn
python .\train.py
cd .\tutorials\homework\lesson3\dqn_mountaincar
python .\train.py
最终DQN结果如下面的GIF所示。
倒立摆(CartPole):
小车上山(MountainCar):
总结
框架库PARL将强化学习框架抽象为: Model、Algorithm、Agent三层,使得强化学习算法的实现和调试更方便和灵活。前两者尤其针对deep RL的情况,有神经网络时直接调用paddle的api可以很方便的进行网络和算法的构建。本文由强化学习经典算法Sarsa和Q-learning扩展到deep RL的DQN算法,并以DQN为例讲解了PARL的使用方法。下篇文章我会讲基于policy的PG算法和用于连续状态控制的DDPG,敬请期待。