写在前面
不同于工程界常用的DH参数(Denavit-Hartenberg parameters),学术界比较常用的机械臂建模方法为指数乘积公式POE(The product of exponentials formula)。后者的优点是在运动学建模上比DH参数更简洁,可以和李群理论联系起来,方便扩展到动力学建模;缺点是建立的模型和实际机械臂数学上等效,但难以对应关节坐标系。由于该方法的相关介绍在网上比较少,所以我在这篇文章讲一下。
三维刚体运动
本节默认大家对群有一定了解,不懂的参考这里。简单的说群(group)是一种集合加上一种运算的代数结构,而对于李群来说,相应的集合和运算分别为流形(manifold)和左乘。
SO(3)和李群
首先,我们回顾一下特殊正交群(special orthogonal)SO(3),这是一个李群(Lie group),同时也是所有3D旋转矩阵(rotation matrix)的集合。特殊正交群SO(3)对应的李代数(Lie algebra)为所有反对称矩阵(skew-symmetric matrix)的集合so(3)。李代数对应李群的正切空间,它描述了李群局部的导数。如果说SO(3)是个流形(manifold),那么so(3)是流形对应的切空间(tangent space)。
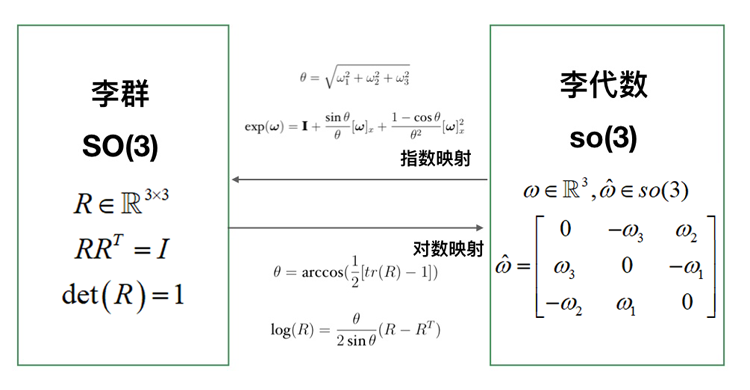
对于刚体旋转,我们通常把SO(3)当作构形空间(configuration space),那么刚体的角速度显然对应so(3),两者的关系如图1所示。
注意:图中ω范数为θ,相当于ωθ且∥ω∥=1。
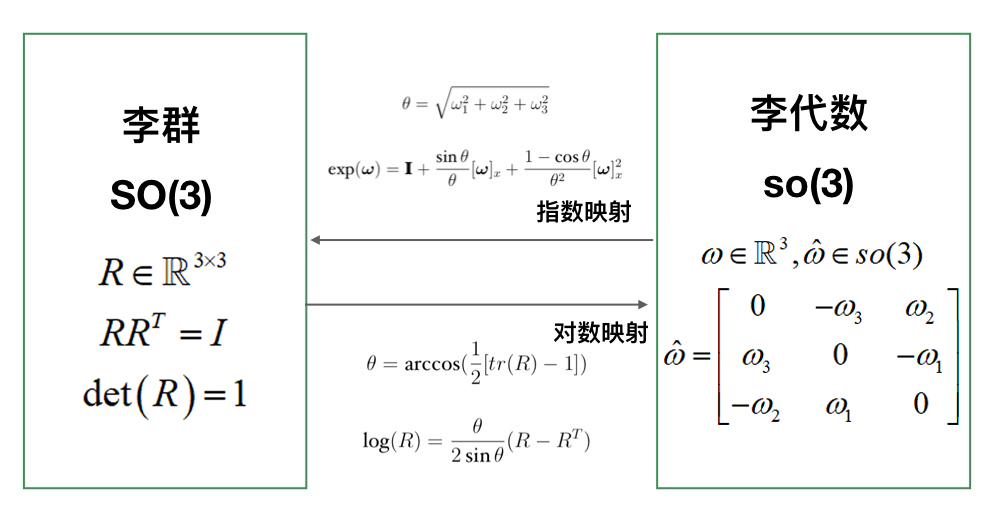
图1. SO(3)和so(3)的关系
定义ωθ∈R3为旋转R的指数坐标(exponential coordinates),由罗德里格斯公式(Rodrigues' formula)可以轻松计算出,当∥ω∥=1时,
R=eω^θ=I+ω^sinθ+ω^2(1−cosθ)。
这意味着,如果我们绕着轴ω以单位速度旋转θ时间,那么净旋转可表示为eω^θ。显然指数坐标不唯一,有如下命题成立。
命题1:给定R∈SO(3),存在ω∈R3,∥ω∥=1和θ∈R,使得R=eω^θ。
SE(3)和螺旋理论
接下来,我们继续讲刚体运动/变换(rigid motion/transformation),包括平动和旋转。刚体运动的构形空间由特殊欧氏群(special Euclidean group)SE(3)={(p,R)}=R3×SO(3)表示,相应的李代数为se(3)。类似的,我们将SE(3)中的构形记作g∈SE(3),并定义运动旋量(twist)为ξ^∈se(3),即
ξ^=[ω^0v0]∈R4×4,
旋量坐标(twist coodinates)为ξ∈R6。定义ξθ∈R6为刚体变换g的指数坐标,也有如下命题成立。
命题2:给定g∈SE(3),存在ξ^∈se(3)(∥ω∥=1)和θ∈R,使得g=eξ^θ。
对于刚体运动,计算g=eξ^θ稍微复杂一些,需要分类讨论,证明见参考文献1的41页命题2.8。
g=eξ^θ=⎩⎪⎪⎪⎨⎪⎪⎪⎧[I0vθ1],[eω^θ0(I−eω^θ)(ω×v)+ωωTvθ1],ω=0,ω=0。
考虑一个螺旋形式的刚体运动,即绕着一个轴旋转θ同时沿着轴向平动d,这样的刚体运动称为螺旋运动(screw motion),如图2所示。
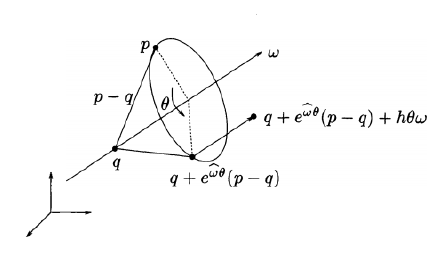
图2. 螺旋运动
定义平动和旋转的比率为h:=d/θ∈R,称为pitch,则螺旋运动在齐次坐标(homogeneous coodinates)下表示为
g[p1]=[eω^θ0(I−eω^θ)q+hθω1][p1]。
因此,相应的运动旋量为
ξ^=[ω^0−ω×q+hω0]。
机械臂运动学
机械臂可以看作是多个刚体组成的多体结构,各个刚体之间由关节(joint)连接。基本关节分为六类,称为低副(lower pairs),包括回转型(revolute)、棱柱型(prismatic)、螺旋型(helical)、圆柱形(cylindrical)、球型(spherical)和平面型(planar)关节。
对于常见机械臂,我们只需关注回转型和棱柱型即可,它们的运动旋量分别表示为
ξ=[−ω×qω](h=0),ξ=[v0](h=∞),
其中ω∈R3是旋转轴向的单位向量,q∈R3是轴上任意一点,v∈R3是平动方向的单位向量。所有向量均关于基坐标系S(base frame)给出。
前向运动学
机械臂操作中,末端执行器的构形是我们最关心的,因此定义末端坐标系T(tool frame)。给定一系列关节坐标(joint variables)θ∈Q,Q是关节空间(joint space),前向动力学(forward kinematics)由映射gst:Q→SE(3)表示,该映射描述了末端坐标系相对基坐标系的构形。
考虑单自由度机械臂,即只有一个关节,其前向动力学为
gst(θ)=eξ^θgst(0)。
这意味着,通过一个螺旋运动eξ^θ,机械臂末端构形由gst(0)变为gst(θ)。
同理,对于n自由度机械臂,其前向动力学为
gst(θ)=eξ^1θ1eξ^2θ2⋯eξ^nθngst(0),
称为指数乘积公式(the product of exponentials formula)。
POE和DH参数的关系
DH参数也可以写成螺旋运动的组合
gst(θ)=gl0l1(θ1)gl1l2(θ2)⋯gln−1ln(θn)glnt,
其中gli−1li=eξ^i−1,iθigli−1li(0)由四个刚体运动组合而成,即Tz(di)Rz(ϕi)Tx(ai)Rx(αi)。对于回转关节,ϕi=θi;对于棱柱关节,di=θi。
注意:ξi转化为(di,ϕi,ai,αi)的方法不唯一,这里给出一个参考文献。
为了研究ξi−1,i和ξi之间的关系,我们先定义伴随变换(adjoint transformation)。如果说gab定义两个坐标系A,B之间的刚体运动变换,即ga=gabgb,那么伴随变换则定义了它们之间的刚体速度(rigid body velocity)变换,即Vaba=AdgabVabb,其定义为
Adgab=[Rab0p^abRabRab]。
ξi−1,i和ξi之间的关系可表示为ξi=Adgl0li−1(0)ξi−1,i,证明见参考文献1的93页。