• 写在前面
• virtual linkage模型
• 内力的计算
• 两个机械臂搬运实例
• 源代码

写在前面

上一篇文章(机械臂协同搬运中的阻抗控制)有一点遗留部分没有讲，即内力$F_{int}$应该如何建模。我们知道，$F_{int}$在抓持矩阵$G$的零空间里，即$GF_{int}=0$。如何选取一个有实际物理意义的模型，同时能够满足前述等式约束呢？这篇文章就会介绍一个virtual linkage模型^[1]来表示搬运物体的内力。

virtual linkage模型

考虑如图1所示的多机械臂搬运场景。

我们定义virtual linkage的运动学结构为接触点相互连结的3个主动(actuated)的棱柱关节，其中接触点处为被动(passive)的回转关节，它们形成一个闭链(closed-chain)，如图2所示。

内力可以表示为棱柱关节上所作用的力。一般的，对任意virtual linkage，如果它的接触点有$n$个，那么需要$3(n-2)$个棱柱关节。

内力的计算

假设接触点仅受到力作用。令$e_{ij}$为沿着某一个link从接触点$i$到接触点$j$的单位向量，令$r_i$为物体上某一参考点到接触点$i$的向量，如图3所示。

定义$f_i$为施加到接触点$i$上的力，则$\boldsymbol f=[f_1^T,f_2^T,f_3^T]^T$。定义$\boldsymbol t=[t_1^T,t_2^T,t_3^T]^T$，满足

$\boldsymbol f=-E\boldsymbol t+\boldsymbol f_e，$

其中

$E=\begin{bmatrix} -e_{12}&0&e_{31}\\ e_{12}&-e_{23}&0\\ 0&e_{23}&-e_{31} \end{bmatrix}。$

定义上外力$\boldsymbol f_e$不产生内力，故$\boldsymbol t=-\bar E\boldsymbol f$，$\bar E \boldsymbol f_e=0$，其中$\bar E=(E^TE)^{-1}E^T$为$E$的左逆。

物体的合力$f_r$和合力矩$m_r$为

$\begin{bmatrix} f_r\\ m_r \end{bmatrix}=G\boldsymbol f，$

其中

$G=\begin{bmatrix} I_3&I_3&I_3\\ \hat r_1&\hat r_2&\hat r_3 \end{bmatrix}。$

注意：

• 我在$E\boldsymbol t$前加了负号，因为按图3的定义$E\boldsymbol t$是由接触点作用于机械臂末端的力，而$\boldsymbol{f}$是机械臂末端作用于接触点的力，二者方向相反。
• 按照上面定义的方向，当$\boldsymbol t>0$时，物体受到压力，此时反作用力的方向与$E$中的向量同向。
• 这里的$r_i$和$e_{ij}$均为时变的，所以每次计算都要更新$E$和$G$。
• 这里假设抓持点固定，所以$E$和$G$虽然时变，但是仍满足刚体运动性质(向量模不变)。
• $E$位于$G$的零空间，即$GF_{int}=GEt=0$。

两个机械臂搬运实例

下面我们将virtual linkage应用到两个机械臂搬运任务中，如图4所示。

我们可以写出施加的力和内力之间的关系

$\begin{bmatrix} f_1\\ f_2 \end{bmatrix}=-Et_{12}，$

其中$E=[-1,0,0,1,0,0]^T$。

这里将物体对接触点产生的反作用力$t_{12}$建模为弹簧模型。令实际接触点位置为$x_1$、$x_2$，有如下关系

$t_{12}= -k_t(\|x_1-x_2\|-\|r_1-r_2\|) 。$

反过来已知$f_1$、$f_2$，可由$\bar E=\frac{1}{2}[-1,0,0,1,0,0]^T$计算得到

$t_{12}=-\bar E\begin{bmatrix} f_1\\ f_2 \end{bmatrix}。$

MATLAB代码如下：

%% contact positions
x0 = [-1,1.5,0;
    0,1.5,0];

%% object position
Xo = [sum(x0)/size(x0,1),0,0,0];

%% displacements
ro= x0-Xo(1:3);
r = @(Xo,i) (SO3.rpy(Xo(4:6))*ro(i,:)')';

%% object impedance
Mo = blkdiag(obj.mass*eye(3),obj.inertia);
Co = @(dXo) [-obj.mass*g';skew(dXo(4:6))*obj.inertia*dXo(4:6)'];
G = @(Xo) [eye(3),eye(3);
    skew(r(Xo,1)),skew(r(Xo,2))];

%% virtual linkage
e12 = @(Xo) (r(Xo,2)-r(Xo,1))/norm(r(Xo,1)-r(Xo,2));
E = @(Xo) [-e12(Xo),e12(Xo)]'; 
% modeled as a spring
Kpe = 1;
f12 = @(x) Kpe*(norm(x(1,:)-x(2,:))-norm(ro(1,:)-ro(2,:)));
Fint = @(Xo) (E(Xo)*f12(x))';

%% command force
Fcmd = @(Xo,dXo,Xd) (pinv(G(Xo))*(Co(dXo)+Mo*md^-1*Fimp(Xo,dXo,Xd)')+Fint(Xo)')'; 

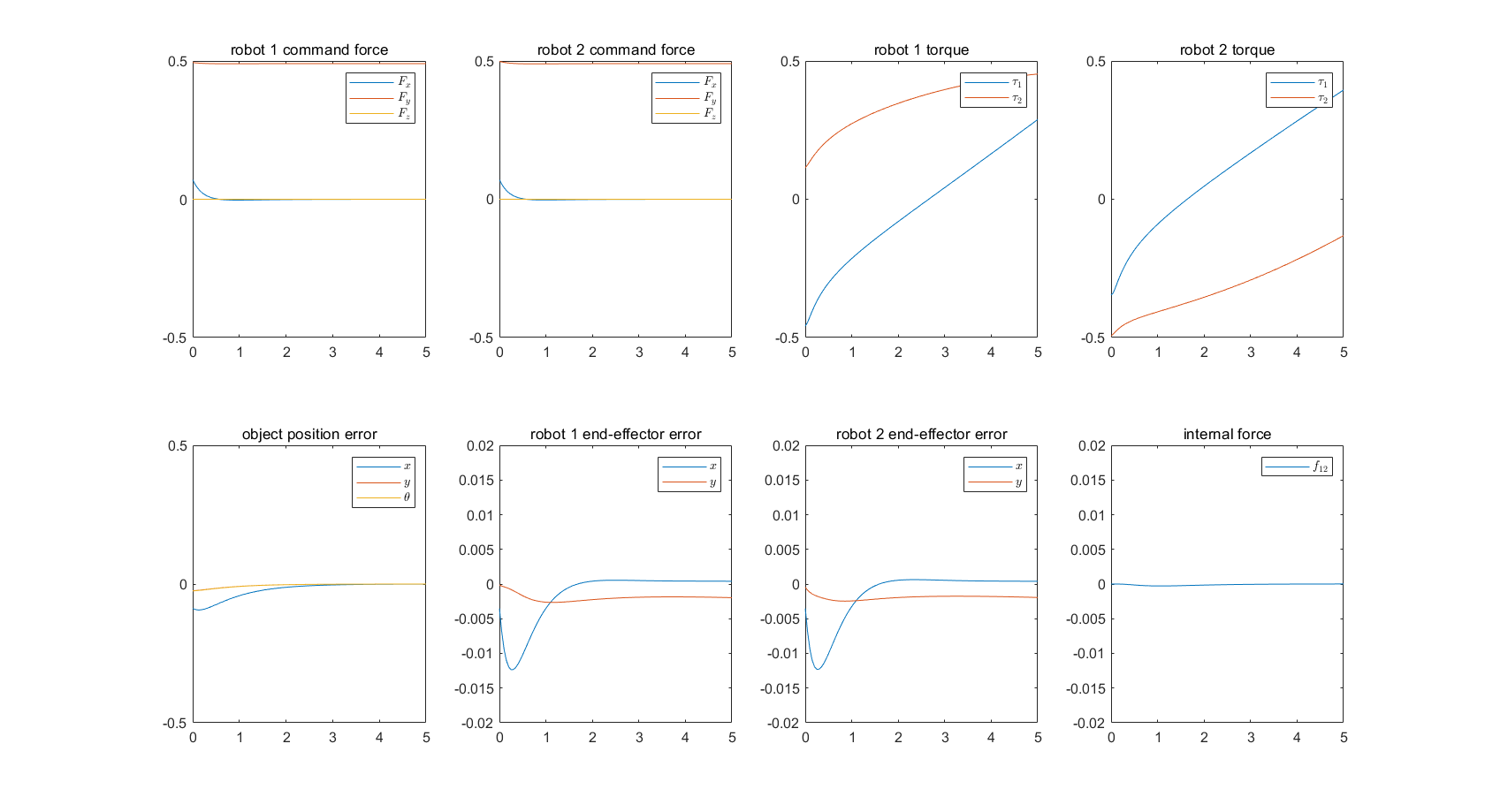
结果下图所示。

源代码

本文所需全部源代码已上传至我的GitHub，点击这里下载。与上一篇文章(机械臂协同搬运中的阻抗控制)相同，运行two_link_object.m和two_link_distributed.m即可。使用前请确认RTB已经正确安装，下载和安装说明点击这里。

如果喜欢，欢迎点赞和fork。