写在前面
原论文:A Decentralized Controller-Observer Scheme for Multi-Agent Weighted Centroid Tracking。
本文是Antonelli 2013的总结,主要介绍了一种控制器和观测器结合的分布式加权质心跟踪方法,其中每一个智能体都通过观测器估计所有智能体的状态。
问题描述
定义x = [ x 1 T , ⋯ , x n T ] T x=[x_1^T,\cdots,x_n^T]^T x = [ x 1 T , ⋯ , x n T ] T
x ˙ = u ( 1 ) \dot x=u\qquad (1)
x ˙ = u ( 1 )
控制目标是加权质心跟踪:
σ ( x ) = ∑ i = 1 n w i x i → σ d \sigma(x)=\sum_{i=1}^nw_ix_i\to\sigma_d
σ ( x ) = i = 1 ∑ n w i x i → σ d
状态观测器
令Π i ∈ R n d × n d \Pi_i\in\mathbb R^{nd\times nd} Π i ∈ R n d × n d Π i = diag { O d , ⋯ , I d , ⋯ , O d } \Pi_i=\operatorname{diag}\{O_d,\cdots,I_d,\cdots,O_d\} Π i = d i a g { O d , ⋯ , I d , ⋯ , O d } i i i ∑ i = 1 n Π i = I n d \sum_{i=1}^n\Pi_i=I_{nd} ∑ i = 1 n Π i = I n d
智能体i i i
i x ^ ˙ = k o ( ∑ j ∈ N i ( j x ^ − i x ^ ) + Π i ( x − i x ^ ) ) + i u ^ ( 2 ) ^i\dot {\hat x}=k_o\left(\sum_{j\in\mathcal N_i}({^j\hat x}-{^i\hat x})+\Pi_i(x-{^i\hat x})\right)+{^i\hat u}\qquad (2)
i x ^ ˙ = k o ⎝ ⎛ j ∈ N i ∑ ( j x ^ − i x ^ ) + Π i ( x − i x ^ ) ⎠ ⎞ + i u ^ ( 2 )
其中k o > 0 k_o>0 k o > 0
i x ^ = [ i x ^ 1 i x ^ 2 ⋮ i x ^ n ] , i u ^ = [ i u ^ 1 i u ^ 2 ⋮ i u ^ n ] ∈ R n d . ^i\hat x=\begin{bmatrix}
^i\hat x_{1}\\
^i\hat x_{2}\\
\vdots\\
^i\hat x_{n}
\end{bmatrix},\quad ^i\hat u=\begin{bmatrix}
^i\hat u_{1}\\
^i\hat u_{2}\\
\vdots\\
^i\hat u_{n}
\end{bmatrix}\in\mathbb R^{nd}.
i x ^ = ⎣ ⎢ ⎢ ⎢ ⎡ i x ^ 1 i x ^ 2 ⋮ i x ^ n ⎦ ⎥ ⎥ ⎥ ⎤ , i u ^ = ⎣ ⎢ ⎢ ⎢ ⎡ i u ^ 1 i u ^ 2 ⋮ i u ^ n ⎦ ⎥ ⎥ ⎥ ⎤ ∈ R n d .
注意到,每一个智能体只用到了局部信息,因为Π i \Pi_i Π i i i i
简洁起见,将(2)写成矩阵形式
x ^ ˙ = − k o L x ^ + k o Π x ~ + u ^ ( 3 ) \dot {\hat {\boldsymbol x}}=-k_o\boldsymbol L \hat {\boldsymbol x}+k_o\boldsymbol \Pi\tilde {\boldsymbol x}+\hat {\boldsymbol u}\qquad (3)
x ^ ˙ = − k o L x ^ + k o Π x ~ + u ^ ( 3 )
其中L = L ⊗ I n d \boldsymbol L=L\otimes I_{nd} L = L ⊗ I n d Π = diag { Π 1 , ⋯ , Π n } \boldsymbol \Pi=\operatorname{diag}\{\Pi_1,\cdots,\Pi_n\} Π = d i a g { Π 1 , ⋯ , Π n } 估计状态误差 和估计控制输入 定义如下
x ~ = [ 1 x ~ ⋮ n x ~ ] = [ x − 1 x ^ ⋮ x − n x ^ ] = 1 n ⊗ x − x ^ , u ^ = [ 1 u ^ ⋮ n u ^ ] ∈ R n 2 d \tilde {\boldsymbol x}=\begin{bmatrix}
^1\tilde x\\
\vdots\\
^n\tilde x
\end{bmatrix}=\begin{bmatrix}
x-{^1\hat x}\\
\vdots\\
x-{^n\hat x}
\end{bmatrix}=1_n\otimes x-\hat {\boldsymbol x},\quad \hat {\boldsymbol u}=\begin{bmatrix}
^1\hat u\\
\vdots\\
^n\hat u
\end{bmatrix}\in\mathbb R^{n^2d}
x ~ = ⎣ ⎢ ⎡ 1 x ~ ⋮ n x ~ ⎦ ⎥ ⎤ = ⎣ ⎢ ⎡ x − 1 x ^ ⋮ x − n x ^ ⎦ ⎥ ⎤ = 1 n ⊗ x − x ^ , u ^ = ⎣ ⎢ ⎡ 1 u ^ ⋮ n u ^ ⎦ ⎥ ⎤ ∈ R n 2 d
定义u u u 估计状态误差动力学 为
x ~ ˙ = − k o ( L + Π ) x ~ + 1 n ⊗ u − u ^ ( 4 ) \dot {\tilde {\boldsymbol x}}=-k_o(\boldsymbol L+\boldsymbol \Pi)\tilde {\boldsymbol x}+1_n\otimes u-\hat {\boldsymbol u}\qquad (4)
x ~ ˙ = − k o ( L + Π ) x ~ + 1 n ⊗ u − u ^ ( 4 )
注意到,L + Π \boldsymbol L+\boldsymbol \Pi L + Π
证明L + Π \boldsymbol L+\boldsymbol \Pi L + Π
显然两个矩阵都是半正定的,那么相加也同样是半正定的。如果是正定,除非他们的零空间不相交,即
null ( L ) ∩ null ( Π ) = { 0 n 2 d } . \operatorname{null}(\boldsymbol L)\cap\operatorname{null}(\boldsymbol \Pi)=\{0_{n^2d}\}.
n u l l ( L ) ∩ n u l l ( Π ) = { 0 n 2 d } .
注意到L , Π ∈ R n 2 d × n 2 d \boldsymbol L,\boldsymbol \Pi\in\mathbb R^{n^2d\times n^2d} L , Π ∈ R n 2 d × n 2 d rank ( L ) = n d ( n − 1 ) \operatorname{rank}(\boldsymbol L)=nd(n-1) r a n k ( L ) = n d ( n − 1 ) dim ( null ( L ) ) = n d \dim(\operatorname{null}(\boldsymbol L))=nd dim ( n u l l ( L ) ) = n d null ( L ) \operatorname{null}(\boldsymbol L) n u l l ( L )
null ( L ) = span ( 1 n ⊗ I n d ) \operatorname{null}(\boldsymbol L)=\operatorname{span}(1_n\otimes I_{nd})
n u l l ( L ) = s p a n ( 1 n ⊗ I n d )
其中的向量满足
v L = [ ν T , ⋯ , ν T ] T ∈ R n 2 d , ∀ ν ∈ R n d v_L=[\nu^T,\cdots,\nu^T]^T\in\mathbb R^{n^2d},\quad \forall \nu\in\mathbb R^{nd}
v L = [ ν T , ⋯ , ν T ] T ∈ R n 2 d , ∀ ν ∈ R n d
同样地,我们有rank ( Π ) = n d \operatorname{rank}(\boldsymbol \Pi)=nd r a n k ( Π ) = n d dim ( null ( Π ) ) = n d ( n − 1 ) \dim(\operatorname{null}(\boldsymbol \Pi))=nd(n-1) dim ( n u l l ( Π ) ) = n d ( n − 1 ) null ( Π ) \operatorname{null}(\boldsymbol \Pi) n u l l ( Π )
null ( Π ) = span ( I n 2 d − Π ) \operatorname{null}(\boldsymbol \Pi)=\operatorname{span}( I_{n^2d}-\boldsymbol \Pi)
n u l l ( Π ) = s p a n ( I n 2 d − Π )
其中的向量满足
v Π = [ v 1 T , ⋯ , v n T ] T ∈ R n 2 d v i = [ v i , 1 T , ⋯ , v i , n T ] ∈ R n d : ∀ v i , j ∈ R d , v i , i = 0 d v_\Pi=[v_1^T,\cdots,v_n^T]^T\in\mathbb R^{n^2d}\\
v_i=[v_{i,1}^T,\cdots,v_{i,n}^T]\in\mathbb R^{nd}: \forall v_{i,j}\in\mathbb R^d,v_{i,i}=0_d
v Π = [ v 1 T , ⋯ , v n T ] T ∈ R n 2 d v i = [ v i , 1 T , ⋯ , v i , n T ] ∈ R n d : ∀ v i , j ∈ R d , v i , i = 0 d
比较v L v_L v L v Π v_\Pi v Π v L v_L v L null ( Π ) \operatorname{null}(\boldsymbol \Pi) n u l l ( Π ) v Π v_\Pi v Π null ( L ) \operatorname{null}(\boldsymbol L) n u l l ( L )
经典consensus算法
网络化系统中,只要有一个节点知道参考信息,而拓扑又是连通的,那么就可以利用经典consensus算法使得参考信息传递到整个网络中,有兴趣可以比较一下,这里不继续讨论。
i x ^ ˙ k = 1 i b k + ∑ j = 1 n a i j ( ∑ j ∈ N i a i j ( j x ^ ˙ k − γ ( i x ^ k − j x ^ k ) ) + i b k ( x ˙ k − γ ( i x ^ k − x k ) ) ) ^i\dot {\hat x}_k=\frac{1}{{^ib}_k+\sum_{j=1}^n a_{ij}}\left(\sum_{j\in\mathcal N_i} a_{ij}({^j\dot {\hat x}}_k-\gamma({^i\hat x}_k-{^j\hat x}_k))+{^ib}_k(\dot x_k-\gamma({^i\hat x_k}-x_k))\right)
i x ^ ˙ k = i b k + ∑ j = 1 n a i j 1 ⎝ ⎛ j ∈ N i ∑ a i j ( j x ^ ˙ k − γ ( i x ^ k − j x ^ k ) ) + i b k ( x ˙ k − γ ( i x ^ k − x k ) ) ⎠ ⎞
其中i b k = 1 ^ib_k=1 i b k = 1 i = k i=k i = k i b k = 0 ^ib_k=0 i b k = 0 k = 1 , ⋯ , n k=1,\cdots,n k = 1 , ⋯ , n
加权质心跟踪算法
定义w = [ w 1 , ⋯ , w n ] T w=[w_1,\cdots,w_n]^T w = [ w 1 , ⋯ , w n ] T w = w ⊗ I d \boldsymbol w=w\otimes I_d w = w ⊗ I d σ ˙ = w T x ˙ \dot \sigma=\boldsymbol w^T\dot x σ ˙ = w T x ˙ u 0 ∈ R n d u_0\in\mathbb R^{nd} u 0 ∈ R n d
u 0 = ( w T ) † ( σ ˙ d − k c ( σ ( x ) − σ d ) ) ( 5 ) u_0=(\boldsymbol w^T)^\dagger(\dot \sigma_d-k_c(\sigma(x)-\sigma_d))\qquad (5)
u 0 = ( w T ) † ( σ ˙ d − k c ( σ ( x ) − σ d ) ) ( 5 )
其中k c > 0 k_c>0 k c > 0 ( w T ) † = ( 1 / ∥ w ∥ 2 ) w (w^T)^\dagger=(1/\|w\|^2)w ( w T ) † = ( 1 / ∥ w ∥ 2 ) w w T ( w T ) † = I n w^T(w^T)^\dagger=I_n w T ( w T ) † = I n
受(5)启发,可以分布式设计智能体i i i u i = i u ^ i ∈ R d u_i={^i\hat u_i\in\mathbb R^d} u i = i u ^ i ∈ R d
u i = i u ^ i = w i ∥ w ∥ 2 ( σ ˙ d − k c ( σ ( i x ^ ) − σ d ) ( 6 ) u_i={^i\hat u_i}=\frac{w_i}{\|w\|^2}(\dot \sigma_d-k_c(\sigma({^i\hat x})-\sigma_d)\qquad (6)
u i = i u ^ i = ∥ w ∥ 2 w i ( σ ˙ d − k c ( σ ( i x ^ ) − σ d ) ( 6 )
由于智能体i i i
相应的,智能体i i i
i u ^ j = w j ∥ w ∥ 2 ( σ ˙ d − k c ( σ ( i x ^ ) − σ d ) ( 7 ) ^i\hat u_j=\frac{w_j}{\|w\|^2}(\dot \sigma_d-k_c(\sigma({^i\hat x})-\sigma_d)\qquad (7)
i u ^ j = ∥ w ∥ 2 w j ( σ ˙ d − k c ( σ ( i x ^ ) − σ d ) ( 7 )
闭环动力学
定义u = [ u 1 T , ⋯ , u n T ] T = [ 1 u ^ 1 T , ⋯ , n u ^ n T ] T u=[u_1^T,\cdots,u_n^T]^T=[{^1\hat u_1^T},\cdots,{^n\hat u_n^T}]^T u = [ u 1 T , ⋯ , u n T ] T = [ 1 u ^ 1 T , ⋯ , n u ^ n T ] T
j u ^ j − i u ^ j = k c w j ∥ w ∥ 2 w T ( i x ^ − j x ^ ) = k c w j ∥ w ∥ 2 w T ( j x ~ − i x ~ ) ( 8 ) ^j\hat u_j-{^i\hat u_j}=k_c\frac{w_j}{\|w\|^2}\boldsymbol w^T({^i\hat x}-{^j\hat x})=k_c\frac{w_j}{\|w\|^2}\boldsymbol w^T({^j\tilde x}-{^i\tilde x})\qquad (8)
j u ^ j − i u ^ j = k c ∥ w ∥ 2 w j w T ( i x ^ − j x ^ ) = k c ∥ w ∥ 2 w j w T ( j x ~ − i x ~ ) ( 8 )
所以如下等式成立:
u − i u ^ = − k c w w T ∥ w ∥ 2 i x ~ + k c diag ( w ) ⊗ w T ∥ w ∥ 2 x ~ = : − A o i x ~ + B o x ~ ( 9 ) u-{^i\hat u}=-k_c\frac{\boldsymbol w\boldsymbol w^T}{\|w\|^2}{^i\tilde x}+k_c\frac{\operatorname{diag}(w)\otimes\boldsymbol w^T}{\|w\|^2}\tilde {\boldsymbol x}=:-A_o{^i\tilde x}+B_o\tilde {\boldsymbol x}\qquad(9)
u − i u ^ = − k c ∥ w ∥ 2 w w T i x ~ + k c ∥ w ∥ 2 d i a g ( w ) ⊗ w T x ~ = : − A o i x ~ + B o x ~ ( 9 )
其中A o ∈ R n d × n d A_o\in\mathbb R^{nd\times nd} A o ∈ R n d × n d B o ∈ R n d × n 2 d B_o\in\mathbb R^{nd\times n^2d} B o ∈ R n d × n 2 d
将估计状态误差动力学 (4)重写为
x ~ ˙ = − k o ( L + Π ) x ~ − ( A o − B o ) x ~ ( 10 ) \dot {\tilde {\boldsymbol x}}=-k_o(\boldsymbol L+\boldsymbol \Pi)\tilde {\boldsymbol x}-(\boldsymbol A_o-\boldsymbol B_o)\tilde {\boldsymbol x}\qquad (10)
x ~ ˙ = − k o ( L + Π ) x ~ − ( A o − B o ) x ~ ( 1 0 )
其中A o = I n ⊗ A o \boldsymbol A_o=I_n\otimes A_o A o = I n ⊗ A o B o = 1 n ⊗ B o \boldsymbol B_o=1_n\otimes B_o B o = 1 n ⊗ B o
由(6)可得,
σ ~ ˙ = σ ˙ d − σ ˙ = σ ˙ d − ∑ i = 1 n w i x ˙ i = σ ˙ d − ∑ i = 1 n w i 2 ∥ w ∥ 2 ( σ ˙ d − k c ( σ ( i x ^ ) − σ d ) = − k c σ ~ − k c ∥ w ∥ 2 ∑ i = 1 n w i 2 w T ( x − i x ^ ) = − k c σ ~ − k c ∥ w ∥ 2 w T ∑ i = 1 n w i 2 i x ~ \begin{aligned}
\dot {\tilde \sigma}&=\dot \sigma_d-\dot \sigma=\dot \sigma_d-\sum_{i=1}^n w_i\dot x_i\\
&=\dot \sigma_d-\sum_{i=1}^n\frac{w_i^2}{\|w\|^2}(\dot \sigma_d-k_c(\sigma({^i\hat x})-\sigma_d)\\
&=-k_c\tilde \sigma-\frac{k_c}{\|w\|^2}\sum_{i=1}^n w_i^2\boldsymbol w^T(x-{^i\hat x})\\
&=-k_c\tilde \sigma-\frac{k_c}{\|w\|^2}\boldsymbol w^T\sum_{i=1}^n w_i^2{^i\tilde x}
\end{aligned}
σ ~ ˙ = σ ˙ d − σ ˙ = σ ˙ d − i = 1 ∑ n w i x ˙ i = σ ˙ d − i = 1 ∑ n ∥ w ∥ 2 w i 2 ( σ ˙ d − k c ( σ ( i x ^ ) − σ d ) = − k c σ ~ − ∥ w ∥ 2 k c i = 1 ∑ n w i 2 w T ( x − i x ^ ) = − k c σ ~ − ∥ w ∥ 2 k c w T i = 1 ∑ n w i 2 i x ~
因此,跟踪误差动力学 可写为
σ ~ ˙ = − k c σ ~ − B c x ~ ( 11 ) \dot {\tilde \sigma}=-k_c\tilde \sigma-\boldsymbol B_c\tilde {\boldsymbol x}\qquad(11)
σ ~ ˙ = − k c σ ~ − B c x ~ ( 1 1 )
其中B c = k c ∥ w ∥ 2 w T ( w T diag { w } ⊗ I n ) ∈ R d × n 2 d \boldsymbol B_c=\frac{k_c}{\|w\|^2}\boldsymbol w^T(\boldsymbol w^T\operatorname{diag}\{\boldsymbol w\}\otimes I_n)\in \mathbb R^{d\times n^2d} B c = ∥ w ∥ 2 k c w T ( w T d i a g { w } ⊗ I n ) ∈ R d × n 2 d
收敛性分析
定义李雅普诺夫函数
V = V o + δ V c = 1 2 x ~ T x ~ + δ 2 σ ~ T σ ~ ( 12 ) V=V_o+\delta V_c=\frac{1}{2}\tilde {\boldsymbol x}^T\tilde {\boldsymbol x}+\frac{\delta}{2}\tilde \sigma^T\tilde \sigma\qquad (12)
V = V o + δ V c = 2 1 x ~ T x ~ + 2 δ σ ~ T σ ~ ( 1 2 )
其中δ > 0 \delta>0 δ > 0
易知V V V
c m ∥ [ x ~ σ ~ ] ∥ 2 ≤ V ≤ c M ∥ [ x ~ σ ~ ] ∥ 2 ( 13 ) c_m\left\|\begin{bmatrix}
\tilde {\boldsymbol x}\\
\tilde \sigma
\end{bmatrix}\right\|^2\leq V\leq c_M\left\|\begin{bmatrix}
\tilde {\boldsymbol x}\\
\tilde \sigma
\end{bmatrix}\right\|^2\qquad (13)
c m ∥ ∥ ∥ ∥ [ x ~ σ ~ ] ∥ ∥ ∥ ∥ 2 ≤ V ≤ c M ∥ ∥ ∥ ∥ [ x ~ σ ~ ] ∥ ∥ ∥ ∥ 2 ( 1 3 )
对任意c m ≤ min { 1 , δ } / 2 c_m\leq \min\{1,\delta\}/2 c m ≤ min { 1 , δ } / 2 c M ≥ max { 1 , δ } / 2 c_M\geq \max\{1,\delta\}/2 c M ≥ max { 1 , δ } / 2
由(10),V o V_o V o
V ˙ o = − k o x ~ T ( L + Π ) x ~ − x ~ ( A o − B o ) x ~ ( 14 ) \dot V_o=-k_o\tilde {\boldsymbol x}^T(\boldsymbol L+\boldsymbol \Pi)\tilde {\boldsymbol x}-\tilde {\boldsymbol x}(\boldsymbol A_o-\boldsymbol B_o)\tilde {\boldsymbol x}\qquad (14)
V ˙ o = − k o x ~ T ( L + Π ) x ~ − x ~ ( A o − B o ) x ~ ( 1 4 )
由于L + Π \boldsymbol L+\boldsymbol \Pi L + Π A o \boldsymbol A_o A o
V ˙ o ≤ − λ o ∥ x ~ ∥ 2 + x ~ T B o x ~ ( 15 ) \dot V_o\leq -\lambda_o\|\tilde {\boldsymbol x}\|^2+\tilde {\boldsymbol x}^T\boldsymbol B_o\tilde {\boldsymbol x}\qquad (15)
V ˙ o ≤ − λ o ∥ x ~ ∥ 2 + x ~ T B o x ~ ( 1 5 )
其中λ o = k o λ m \lambda_o=k_o\lambda_m λ o = k o λ m λ m \lambda_m λ m L + Π \boldsymbol L+\boldsymbol \Pi L + Π
由(8)(9),不等式(15)计算得到
V ˙ o ≤ − λ o ∥ x ~ ∥ 2 + k c ∥ w ∥ 2 x ~ T ( 1 n ⊗ ( diag ( w ) ⊗ w T ) ) x ~ = − λ o ∥ x ~ ∥ 2 + k c ∥ w ∥ 2 ∑ j = 1 n ∑ i = 1 n w j i x ~ j T w T j x ~ ≤ − λ o ∥ x ~ ∥ 2 + k c ∥ w ∥ 2 ∑ j = 1 n ∣ w j ∣ ∥ i x ~ ∥ λ M ( w w T ) ∥ j x ~ ∥ ≤ − λ o ∥ x ~ ∥ + k c ∥ w ∥ ∑ i = 1 n ∑ j = 1 n ∣ w j ∣ ∥ i x ~ ∥ ∥ j x ~ ∥ ≤ − λ o ∥ x ~ ∥ + k c ∑ i = 1 n ∑ j = 1 n ∥ i x ~ ∥ ∥ j x ~ ∥ ≤ − λ o ∥ x ~ ∥ + k c ∑ i = 1 n ∑ j = 1 n ∥ i x ~ ∥ 2 ≤ − ( λ o − n k c ) ∥ x ~ ∥ 2 \begin{aligned}
\dot V_o&\leq -\lambda_o\|\tilde {\boldsymbol x}\|^2+\frac{k_c}{\|w\|^2}\tilde {\boldsymbol x}^T(1_n\otimes(\operatorname{diag}(w)\otimes\boldsymbol w^T))\tilde {\boldsymbol x}\\
&= -\lambda_o\|\tilde {\boldsymbol x}\|^2+\frac{k_c}{\|w\|^2}\sum_{j=1}^n\sum_{i=1}^nw_j{^i\tilde { x}}_j^T\boldsymbol w^T{^j\tilde { x}}\\
&\leq -\lambda_o\|\tilde {\boldsymbol x}\|^2+\frac{k_c}{\|w\|^2}\sum_{j=1}^n|w_j|\| {^i\tilde { x}}\|\sqrt{\lambda_M(ww^T)}\|{^j\tilde { x}}\|\\
&\leq -\lambda_o\|\tilde {\boldsymbol x}\|+\frac{k_c}{\|w\|}\sum_{i=1}^n\sum_{j=1}^n|w_j|\|{^i\tilde { x}}\|\|{^j\tilde { x}}\|\\
&\leq -\lambda_o\|\tilde {\boldsymbol x}\|+k_c\sum_{i=1}^n\sum_{j=1}^n\|{^i\tilde { x}}\|\|{^j\tilde { x}}\|\\
&\leq -\lambda_o\|\tilde {\boldsymbol x}\|+k_c\sum_{i=1}^n\sum_{j=1}^n\|{^i\tilde { x}}\|^2\\
&\leq -(\lambda_o-nk_c)\|{\tilde {\boldsymbol x}}\|^2
\end{aligned}
V ˙ o ≤ − λ o ∥ x ~ ∥ 2 + ∥ w ∥ 2 k c x ~ T ( 1 n ⊗ ( d i a g ( w ) ⊗ w T ) ) x ~ = − λ o ∥ x ~ ∥ 2 + ∥ w ∥ 2 k c j = 1 ∑ n i = 1 ∑ n w j i x ~ j T w T j x ~ ≤ − λ o ∥ x ~ ∥ 2 + ∥ w ∥ 2 k c j = 1 ∑ n ∣ w j ∣ ∥ i x ~ ∥ λ M ( w w T ) ∥ j x ~ ∥ ≤ − λ o ∥ x ~ ∥ + ∥ w ∥ k c i = 1 ∑ n j = 1 ∑ n ∣ w j ∣ ∥ i x ~ ∥ ∥ j x ~ ∥ ≤ − λ o ∥ x ~ ∥ + k c i = 1 ∑ n j = 1 ∑ n ∥ i x ~ ∥ ∥ j x ~ ∥ ≤ − λ o ∥ x ~ ∥ + k c i = 1 ∑ n j = 1 ∑ n ∥ i x ~ ∥ 2 ≤ − ( λ o − n k c ) ∥ x ~ ∥ 2
由(11),V c V_c V c
V ˙ c = σ ~ T σ ~ ˙ = σ ~ T ( − k c σ ~ − B c x ~ ) = σ ~ T ( − k c σ ~ − k c ∥ w ∥ 2 w T ∑ i = 1 n w i 2 i x ~ ) ≤ − k c ∥ σ ~ ∥ 2 + k c ∥ w ∥ ∥ σ ~ ∥ ∑ i = 1 n w i 2 ∥ i x ~ ∥ ≤ − k c ∥ σ ~ ∥ 2 + n k c ∥ w ∥ ∥ σ ~ ∥ ∥ x ~ ∥ \begin{aligned}
\dot V_c&=\tilde \sigma^T\dot {\tilde \sigma}=\tilde \sigma^T(-k_c\tilde \sigma-\boldsymbol B_c\tilde {\boldsymbol x})\\
&=\tilde \sigma^T\left(-k_c\tilde \sigma-\frac{k_c}{\|w\|^2}\boldsymbol w^T\sum_{i=1}^nw_i^2{^i\tilde { x}}\right)\\
&\leq -k_c\|\tilde \sigma\|^2+\frac{k_c}{\|w\|}\|\tilde \sigma\|\sum_{i=1}^nw_i^2\|{^i\tilde { x}}\|\\
&\leq -k_c\|\tilde \sigma\|^2+n k_c \|w\| \|\tilde \sigma\|\|{\tilde {\boldsymbol x}}\|\\
\end{aligned}
V ˙ c = σ ~ T σ ~ ˙ = σ ~ T ( − k c σ ~ − B c x ~ ) = σ ~ T ( − k c σ ~ − ∥ w ∥ 2 k c w T i = 1 ∑ n w i 2 i x ~ ) ≤ − k c ∥ σ ~ ∥ 2 + ∥ w ∥ k c ∥ σ ~ ∥ i = 1 ∑ n w i 2 ∥ i x ~ ∥ ≤ − k c ∥ σ ~ ∥ 2 + n k c ∥ w ∥ ∥ σ ~ ∥ ∥ x ~ ∥
因此,李雅普诺夫函数(12)对时间求导得
V ˙ ≤ − [ ∥ x ~ ∥ ∥ σ ~ ∥ ] T [ λ o − n k c − δ n k c ∥ w ∥ / 2 − δ n k c ∥ w ∥ / 2 δ k c ] [ ∥ x ~ ∥ ∥ σ ~ ∥ ] ( 16 ) \dot V\leq -\begin{bmatrix}
\|\tilde {\boldsymbol x}\|\\
\|\tilde {\sigma}\|
\end{bmatrix}^T\begin{bmatrix}
\lambda_o-nk_c&-\delta n k_c\|w\|/2\\
-\delta n k_c\|w\|/2&\delta k_c
\end{bmatrix}\begin{bmatrix}
\|\tilde {\boldsymbol x}\|\\
\|\tilde {\sigma}\|
\end{bmatrix}\qquad (16)
V ˙ ≤ − [ ∥ x ~ ∥ ∥ σ ~ ∥ ] T [ λ o − n k c − δ n k c ∥ w ∥ / 2 − δ n k c ∥ w ∥ / 2 δ k c ] [ ∥ x ~ ∥ ∥ σ ~ ∥ ] ( 1 6 )
则V ˙ \dot V V ˙ λ o = k o λ m > n k c \lambda_o=k_o\lambda_m>nk_c λ o = k o λ m > n k c k o > n k c / λ m k_o>nk_c/\lambda_m k o > n k c / λ m
δ < 4 k o λ m − n k c n 2 k c ∥ w ∥ 2 . \delta<4\frac{k_o\lambda_m -n k_c}{n^2k_c\|w\|^2}.
δ < 4 n 2 k c ∥ w ∥ 2 k o λ m − n k c .
此时(16)中间的矩阵正定,说明系统指数稳定。
MATLAB仿真
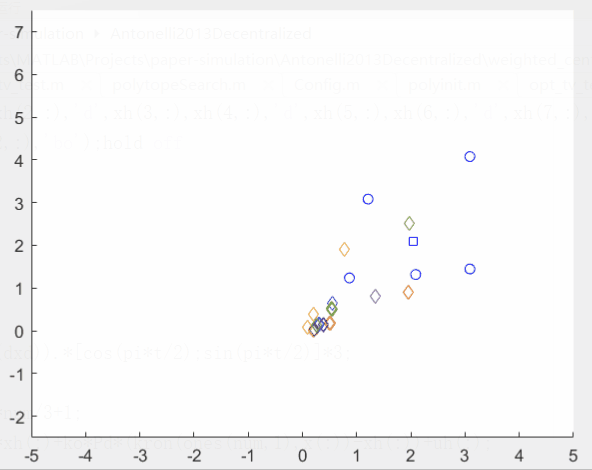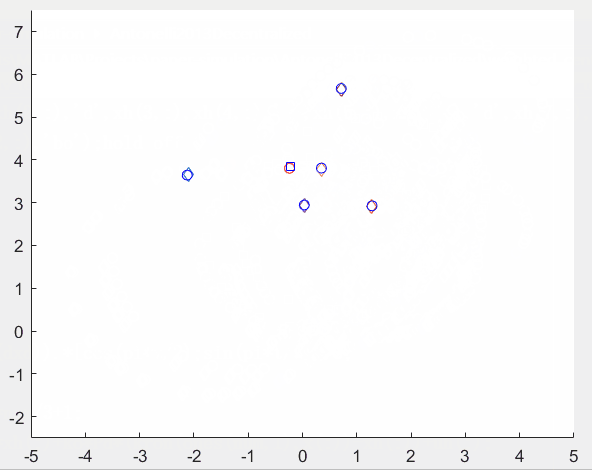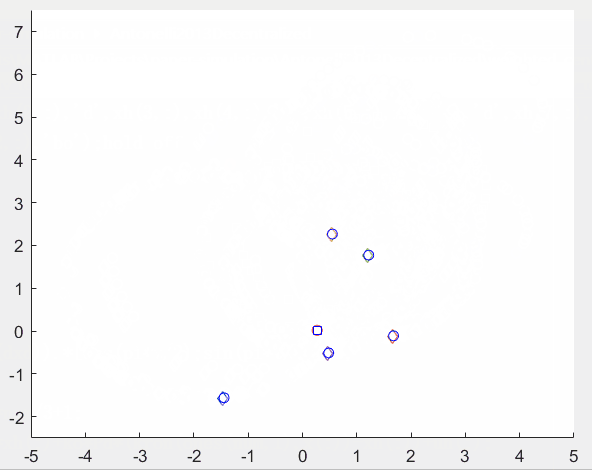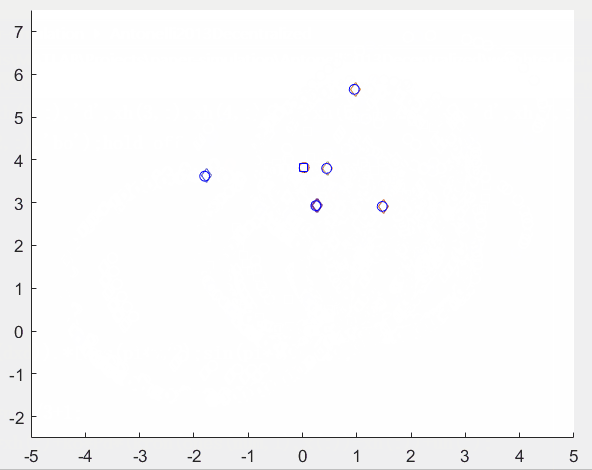
这里简单做了下仿真,蓝色圆圈(bo)是智能体状态,红色圆圈(ro)是质心参考轨迹,蓝色方块(bs)是智能体加权质心,其他同色菱形(d)是所有智能体对某一智能体状态的估计。
仿真结果如图所示。
MATLAB代码和以前一样上传到我的GitHub项目paper-simulation ,运行“weighted_centroid_tracking.m”即可。