• 凸函数
  • 等价条件
  • 常见凸函数
• Lipschitz smooth, strongly convex
  • Lipschitz smooth
    • 定义
    • 等价条件
  • Strongly convex
    • 定义
    • 等价条件
• 拉格朗日函数和对偶函数
• 对偶问题
• KKT条件

凸函数

凸函数(convex function)定义为：$f(x)$的定义域为凸集，且$f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta) f(y)$，$\forall x,y \in \operatorname{dom} f$，$\theta\in[0,1]$。

上述不等式即为Jensen's 不等式：$f(\mathbb E z)\leq \mathbb E f(z)$。

也就是说凸函数判断条件有二：1、convex domain；2、Jensen’s inequality。

等价条件

如果$\operatorname{dom} f$是凸的，判断凸函数的等价条件有：

• 各向皆凸：设$f:\mathbb R^n\to \mathbb R$ ，有映射$g(t)=f(x+tv)$，$\operatorname{dom}g=t|x+tv\in\operatorname{dom}f$，则$f$为凸函数当且仅当$g(t)$对任意$x\in\operatorname{dom} f$，$v\in\mathbb R^n$都是凸函数。
• 一阶条件：对于可导函数，$f$为凸函数当且仅当$f(y)\geq f(x)+\nabla f^T(x)(y-x)$，$\forall x,y\in \operatorname{dom}f$。
• 二阶条件：对于二阶可导函数，$f$为凸函数当且仅当Hessian$\nabla^2f(x)\succeq 0$，$\forall x\in \operatorname{dom} f$。
• epigraph：$f$为凸函数当且仅当epigraph为凸集。epigraph的定义为：$\operatorname{epi} f=\{(x,t)\in\mathbb R^{n+1}|x\in\operatorname{dom} f,\, f(x)\leq t \}$。

一阶条件的几何意义是凸函数上任意点的切线都是凸函数的 under-estimator。因为这个切线仿佛承接住了整个函数$f$， 所以又叫 supporting hyperplane。

二阶条件表明凸函数任意一点“曲度”都是凸的。也可以说梯度是单调的。

• 单调梯度条件：对于可导函数，$f$为凸函数当且仅当$\left(\nabla f(x)-\nabla f(y)\right)^T(x-y)\geq 0$，$\forall x\in \operatorname{dom} f$。

证明：（必要）由一阶条件得，

$\begin{aligned} f(y)&\geq f(x)+\nabla f^T(x)(y-x)\\ f(x)&\geq f(y)+\nabla f^T(y)(x-y) \end{aligned}$

两式相加得证。

（充分）定义$g(t)=f(x+t(y-x))$，那么$g'(t)=\nabla f(x+t(y-x))^T (y-x)$。对于$t \geq 0$, 由于$\big (\nabla f(x) - \nabla f(y)\big )^T (x-y) \geq 0$，所以$g'(t)-g'(0)\geq 0$。则$g(1)-g(0) = \int_0^1 g'(t) dt \geq \int_0^1 g'(0) dt = g'(0)$，
即$f(y) \geq f(x) + \nabla f(x)^T (y-x)$。

常见凸函数

常见凸函数：

• $e^{zx}$在$\mathbb R$上为凸函数，对任意$a\in\mathbb R$成立。
• $x^a$在$\mathbb R_{++}$上为凸函数，如果$a\geq 1$或$a\leq 0$；为凹函数，如果$0\leq a\leq 1$。
• $|x|^p$在$\mathbb R$上为凸函数，如果$p\geq 1$。
• $\log x$在$\mathbb R_{++}$上为凹函数。
• $x\log x$在$\mathbb R_{++}$(或$\mathbb R_{+}$)上为凹函数。

判断复合函数(composition)$f(x)=h(g(x))=h(g_1(x),\cdots,g_k(x))$为凸的方法：

• $f$为凸，如果$h$为凸且对每一个自变数(argument)非减(nondecreasing)，同时$g_i$为凸。
• $f$为凸，如果$h$为凸且对每一个自变数(argument)非增(nonincreasing)，同时$g_i$为凹。
• $f$为凹，如果$h$为凹且对每一个自变数(argument)非减(nondecreasing)，同时$g_i$为凹。

Lipschitz smooth, strongly convex

Lipschitz smooth和strongly convex是证明算法收敛性而假设的常用条件。简单的说，这两条件一上一下，强迫目标凸函数长得像一个二次函数。

Lipschitz smooth

L-smooth表明一个函数的梯度的变化不会太突兀，或者说这个函数比较平滑。

定义

定义如下：

$f$ is $L$-smooth if $\|\nabla f(x) -\nabla f(y)\| \leq L \| x-y\|$ for all $x,y$.

从几何上理解 L-smooth 函数，$f$的下界为超平面，上界为二次函数。如下图所示。

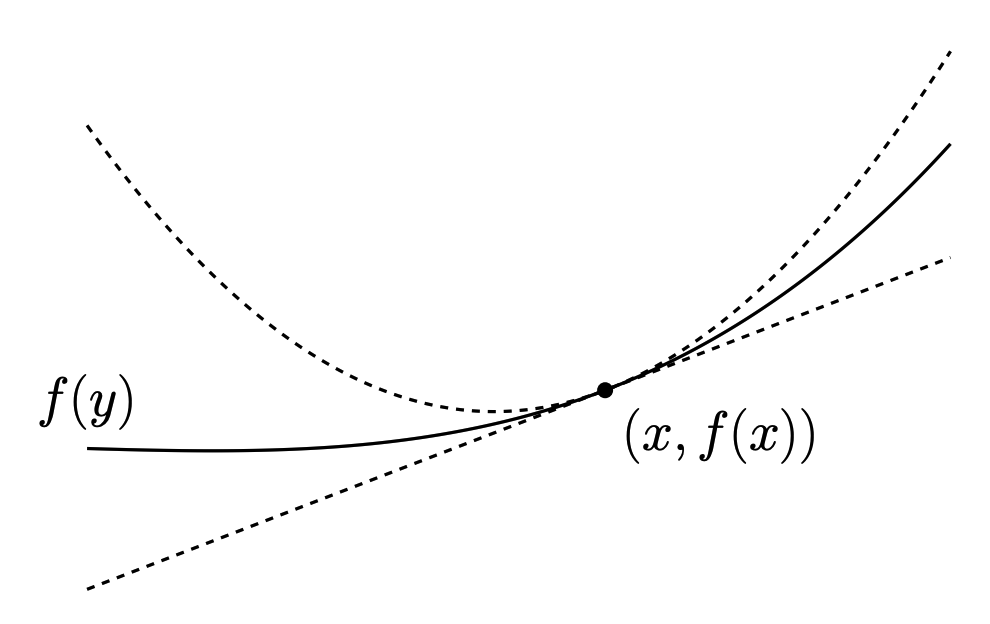
等价条件

等价条件有：

1. $f$ is convex and $L$-smooth.
2. $(\nabla f(x)-\nabla f(y))^T(x-y)\leq L\|x-y\|^2$ for all x, y.
3. $g(x)=\frac{L}{2}x^Tx-f(x)$ is convex.
4. quadratic upper bound: $0\leq f(y)-f(x)-\nabla f(x)^T(y-x)\leq \frac{L}{2}\|x-y\|^2$.
5. $f(y)\geq f(x)+\nabla f(x)^T(y-x)\leq \frac{1}{2L}\|\nabla f(x)-\nabla f(y)\|^2$.
6. co-coercivity: $(\nabla f(x)-\nabla f(y))^T(x-y)\geq \frac{1}{L}\|\nabla f(x)-\nabla f(y)\|^2$ for all x, y.

证明：（1⟹2）两边同乘$\|x-y\|$，由Cauchy-Schwartz不等式，得

$L\|x-y\|^2\geq \|\nabla f(x)-\nabla f(y)\|\|x-y\|\geq (\nabla f(x)-\nabla f(y))^T(x-y)。$

（2⟺3）$(\nabla f(x)-\nabla f(y))^T(x-y)\leq L\|x-y\|=L(x-y)^T(x-y)$，即

$(Lx-\nabla f(x)-Ly+\nabla f(y))^T(x-y)\geq 0，$

即$(\nabla g(x)-\nabla g(y))^T(x-y)\geq 0$。由单调梯度条件，$g$是凸函数。

（3⟺4）由$f$和$g$的一阶条件计算得证。

（4⟺5）令$z=y+\frac{1}{L}(\nabla f(x)-\nabla f(y))$。则

$\begin{aligned} f(y)-f(x)&=f(y)-f(z)+f(z)-f(x)\\ (qub)\quad&\geq -\nabla f(y)^T(z-y)-\frac{L}{2}\|y-z\|^2+\nabla f(x)^T(z-x)\\ &\geq -\frac{1}{L}\nabla f(y)^T(\nabla f(x)-\nabla f(y))-\frac{1}{2L}\|\nabla f(x)-\nabla f(y)\|^2\\ &\quad+\nabla f(x)^T(y-x)+\frac{1}{L}\nabla f(x)^T(\nabla f(x)-\nabla f(y))\\ &=\nabla f(x)^T(y-x)+\frac{1}{2L}\|\nabla f(x)-\nabla f(y)\|^2 \end{aligned}$

（5⟹6）由5得

$\begin{aligned} f(y)&\geq f(x)+\nabla f(x)^T(y-x)+\frac{1}{2L}\|\nabla f(x)-\nabla f(y)\|^2\\ f(x)&\geq f(y)+\nabla f(y)^T(x-y)+\frac{1}{2L}\|\nabla f(x)-\nabla f(y)\|^2 \end{aligned}$

两式相加得6。

（6⟹1）对6的左边使用Cauchy-Schwartz不等式可得L-smooth。

6的右边$\geq 0$，由单调梯度条件可得convex。

Strongly convex

Strongly convex表明一个函数相对二次函数凸的程度。

定义

定义如下：

f is $\mu$-strongly convex if $f(x)-\frac{\mu}{2}x^T x$ is convex.

一个函数减去二次函数仍然是 convex, 说明它至少有这个二次函数这么凸。或者说这个二次函数是它的一个下界。如下图所示。

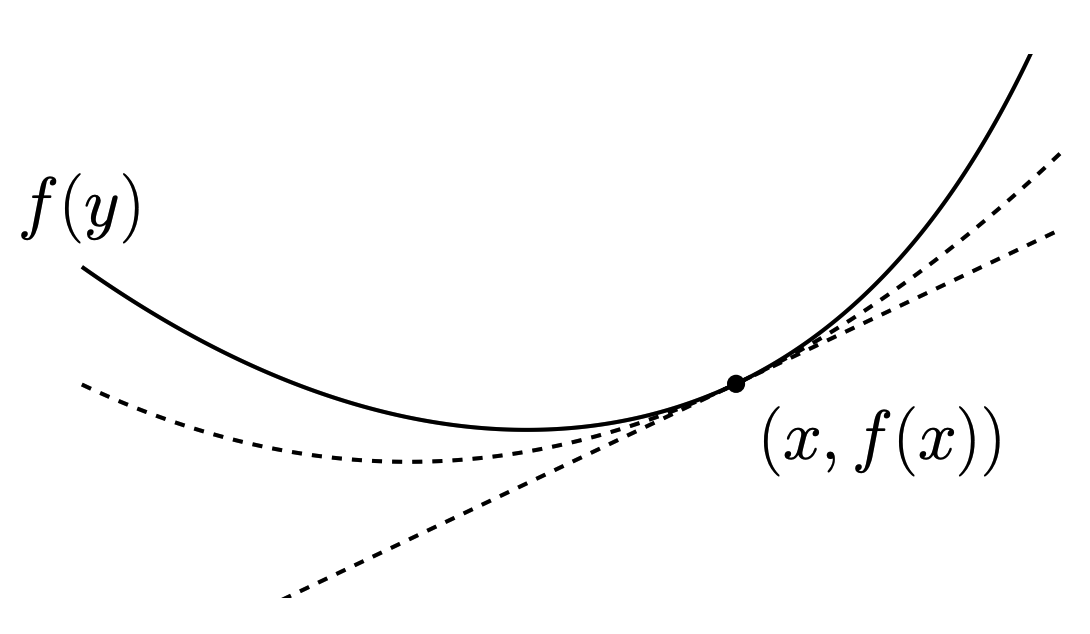
等价条件

1. $f$ is differentiable and $\mu$-strongly convex.
2. $f$ is differentiable and $f(\alpha x +\beta y) \leq \alpha f(x) + \beta f(y) - \frac{\mu \alpha \beta}{2} \|x-y\|^2$ for all $x, y$, for all $\alpha, \beta\geq 0$ s.t. $\alpha + \beta = 1$.
3. (quadratic lower bound): $f(y)\geq f(x) + \nabla f(x)^T (y-x) + \frac{\mu}{2} \|y-x\|^2$.
4. (strong monotonicity or coercivity): $\big (\nabla f(x) - \nabla f(y)\big )^T (x-y) \geq \mu\| x - y \| ^2$.

证明：（1⟺2）对$f(x)-\frac{\mu}{2}x^T x$使用凸函数定义。

（1⟺3）对$f(x)-\frac{\mu}{2}x^T x$使用凸函数一阶条件。

（1⟺4）对$f(x)-\frac{\mu}{2}x^T x$使用凸函数单调梯度条件。

拉格朗日函数和对偶函数

令$x\in\mathbb R^n$，定义域为$\mathcal D$。考虑凸优化问题

$\begin{aligned} \min&\quad f_0(x)\\ \operatorname{s.t.} &\quad f_i(x)\leq 0,\quad i=1,\cdots,m\\ &\quad Ax=b,\quad A\in\mathbb R^{p\times n},\quad p<n. \end{aligned}$

拉格朗日函数(Lagrangian)为

$L(x,\lambda,\nu)=f_0(x)+\lambda^Tf(x)+\nu^T(Ax-b).$

再取下确界得到拉格朗日对偶函数(lagrange dual function)

$g(\lambda,\nu)=\inf_{x\in\mathcal D}\left(f_0(x)+\lambda^Tf(x)+\nu^T(Ax-b)\right).$

对偶函数性质：

• $g(\lambda,\nu)$为凹函数；
• $g(\lambda,\nu)\leq f_0(x^*)$对任意$\lambda\geq0$，$\nu$成立。

对偶函数可以给出原问题最优解的一个不平凡下界，这意味着如果原问题很难求解的时候，我们可以转变思路，求解一个新的优化问题：

$\begin{aligned} \max &\quad g(\lambda,\nu)\\ \operatorname{s.t.} &\quad \lambda\geq 0. \end{aligned}$

常用对偶问题的例子：

对偶问题

令对偶问题的最优解为$g^*$，原问题最优解为$f_0^*$。那么有

• 弱对偶(weak duality)：满足$g^*\leq f_0^*$，无论原问题是否为凸都成立；
• 强对偶(strong duality)：满足$g^*= f_0^*$，如果原问题为凸，一般都成立。在凸优化中，保证强对偶成立的条件被称为constraint qualifications，如Slater's condtion。

Slater's condtion：存在可行解$x\in\operatorname{int} \mathcal D$，使得$Ax=b$，$f_i(x)<0$，$i=1,\cdots,m$。

• 由于存在线性等式约束，因此实际定义域可能不存在内点，可以将这一条件放松为相对内点，即$x\in\operatorname{rint} \mathcal D$；
• 如果不等式约束中存在线性不等式，那么它也不必严格小于0，即$f_i(x)\leq 0$。

KKT条件

由上面的分析，原问题最优解为$f_0^*=\inf_x\sup_{\lambda,\nu}L(x,\lambda,\nu)$，$g^*=\sup_{\lambda,\nu}\inf_x L(x,\lambda,\nu)$。

弱对偶性即max-min不等式：

$\inf_x\sup_{\lambda,\nu}L(x,\lambda,\nu)\geq\sup_{\lambda,\nu}\inf_x L(x,\lambda,\nu)$

强对偶性说明$x,\lambda,\nu$是拉格朗日函数的鞍点。

KKT条件：

$\begin{aligned} Ax^*=b,\quad f_i(x^*)&\leq 0,\quad i=1,\cdots,m\\ \lambda^*&\geq 0\\ \nabla f_0(x^*)+\sum_{i=1}^m\lambda_i^*\nabla f_i(x^*)+A^T\nu^*&=0\\ \lambda_i^*f_i(x^*)&=0,\quad i=1,\cdots,m. \end{aligned}$

如果Slater's condtion满足，那么$x$为最优解当且仅当存在$\lambda,\nu$满足 KKT 条件！